Other 1D potentials

Problem:

A particle confined by a potential energy function which is given by U(x) = c|x|, as shown below.

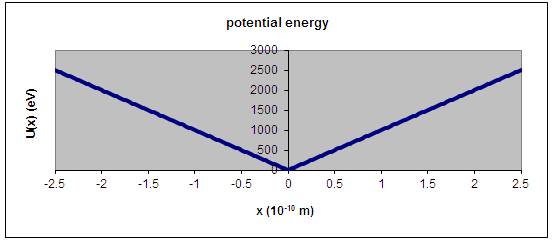
The energy of the ground state is E₀  ~160 eV. The energy of the 6th excited state is E₆ ~960 eV.
The ground state wave function is shown. 

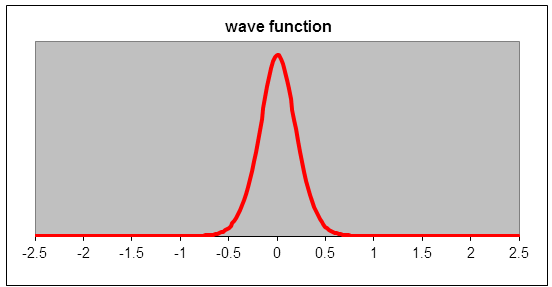
Sketch the wave function of the sixth excited state.  Pay attention to the symmetry, the number of nodes, the wavelength, the amplitude and the boundary condition.  Briefly defend your sketch.

Solution:

• Concepts:
  The 1D time-independent Schroedinger equation.
• Reasoning:
  The wave function of the 6th excited state has 6 nodes.  It is symmetric under reflection about the origin.  The classical turning points are where U(x) = 960 eV, at |x| somewhere between 0.9 and 1 Angstrom.  For |x| < x_{turning point} the wave function oscillates.  Near x = 0 the wave function oscillates rapidly since k is large.  Near the turning points it oscillates less rapidly since k is much smaller.  The amplitude increases as we approach the turning points.   For |x| > x_{turning point} the wave decreases rapidly.
• Details of the calculation:
  

Problem:

Assume that a certain one-dimensional well has just one bound state for an electron.  Now assume that a 1D "crystal" consist of an "infinite" series of such wells, evenly spaced by a distance b.
Let {|n>} be the orthonormal eigenstates of some operator (not the Hamiltonian) that finds the electron located in the nth well, n = -∞ to +∞.
Let us restrict ourselves to the subspace spanned by {|n>}.
Assume that in this basis the matrix elements of the Hamiltonian are given by
<n|H|n> = E₀,  <n|H|m> = -Aδ_m,n±1, i.e. H only couples neighboring state, the electron can move from one well to the next.
(a)  Assume the eigenstates of H are of the form |Φ> = ∑_n a(x_n)|n>.  Write down the coupled linear equations for the a(x_n).  Note that a(x_n±1) = a(x_n ± b).
(b)  Try solutions of the form a(x_n) = exp(ikx_n) and solve for E as a function of k.
Sketch E(k).  Explain why you only need to consider -π/b ≤ k < π/b.
What is the range of possible eigenvalues of H?
(c)  The solutions |Φ> = ∑_n exp(ikx_n)|n> with eigenvalues E(k) are stationary states.  A wave packet with a range of k-values about some k₀ can represent an electron moving through the "crystal".  Find the group velocity of such a wave packet.
(d)  Expand E(k) about k at its minimum value E_min,  keeping terms up to second order in k.
Expand v_g about the same value of k. 
Set E(k) - E_min = ½ m*v_g² and find the effective mass m* of the electron in the crystal near the minimum of the energy band.
Show that m* = ħ²(d²E/dk²)^-1.
(e)  Find the effective mass of the electron in the crystal near the maximum of the energy band.

Solution:

• Concepts:
  Electrons in a periodic structure
• Reasoning:
  We are asked to solve coupled eigenvalue equations.
• Details of the calculation
  (a)  <m|H|Φ> = ∑_n a(x_n) <m|H|n> .
  Ea(x_m) = E₀a(x_m) - Aa(x_m+1) - Aa(x_m-1) = E₀a(x_m) - Aa(x_m + b) - Aa(x_m - b).
  (b)  Eexp(ikx_n) = E₀expik(x_n) - Aexp(ik(x_n+b)) - Aexp(ik(x_n-b)) .
  E = E₀ - Aexp(ikb) - Aexp(-ikb))  = E₀ - 2Acoskb.
  We only need to consider -π/b ≤ k < π/b because k values differing by π/b give the same coefficients.
  The possible eigenvalues of H lie in a band from E₀ - 2A to E₀ + 2A.
  (c)  v_g = dω/dk|_k0 = (1/ħ)dE/dk|_k0 = (2Ab/ħ)sin(k₀b).
  (d)  An expansion of E(k') about k' = 0 for k' = 0 + k yields E(k) = E₀ - 2A + Ak²b² = E_min + Ak²b².
  An expansion of v_g(k') about k' = 0 for k' = 0 + k yields 2Ab²k/ħ.
  E(k) - E_min = Ak²b²  = ½ m*(2Ab/ħ)²k²b²,  m* = ħ²/(2Ab²).
  d²E/dk² = 2Ab².  ħ²(d²E/dk²)^-1 = ħ²/(2Ab²) = m*.
  [For a free wave packet:  v_g = dE/dp = ħ^-1(dE/dk), a = dv_g/dt = ħ^-2(d²E/dk²)d(ħk/dt) = F/m. 
  But F = dp/dt = d(ħk/dt).  Therefore m = ħ²(d²E/dk²)^-1.]
  (e)  And expansion about k' = π/b for k' = π/b - k yields E(k) = E₀ + 2A - Ak²b² = E_max - Ak²b².
  Using m* = ħ²(d²E/dk²)^-1 we find m* = -ħ²/(2Ab²).

Note dv_g/dt = F_ext/m*.  If an external force is applied, the electron in a crystal is subject to this force and internal forces from the lattice.  The net force may point opposite to the external force.