Square potentials, continuum states
Problem:
Consider the one-dimensional potential step defined by
U(x) = 0 , x < 0, U(x) = U0, x > 0.
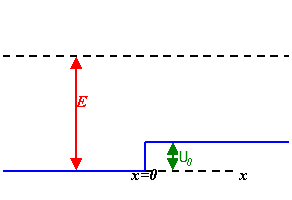
Suppose a wave incident from the left has energy E = 4U0.
What is the probability that the wave will be reflected?
Solution:
- Concepts:
This is a "square potential" problem. We solve HΦ(x)
= EΦ(x) in regions where U(x) is constant and apply boundary conditions.
- Reasoning:
We are given a piecewise constant potential. We have a potential that
has a value of 0 for x < 0 and a value of U0 (barrier) for
x > 0. We are asked to find the reflectance R.
- Details of the calculation:
We have E > U0.
The most general solutions in regions 1, and 2 are
Φ1(x) = A1exp(ik1x) + A1'exp(-ik1x),
Φ2(x) = A2exp(ik2x),
for particles incident from the left.
Here k12 = (2m/ħ2)E and k22
= (2m/ħ2)(E - U0).
Φ is continuous at x = 0.
Therefore A1 + A1' = A2.
(∂/∂x)Φ(x) is continuous at x = 0.
Therefore ik1A1 - ik1A1' = ik2A2 .
We can then solve for A1'/A1 = (k1 - k2)/(k1
+ k2).
The reflectance R
= |A1'/A1|2 = 1 - 4k1k2/(k1 + k2)2.
k12 = 8mU0/ħ2, k22
= 6mU0/ħ2, k1k2 =
(48)½(mU0/ħ2), R = 1 - 4(48)½/(√8
+ √6)2 = 0.005
Problem:
Consider a one-dimensional step potential, of the form
U(x) = 0 for x < 0,
U(x) = U0 for x > 0, with U0 > 0.
A particle with mass m and energy E > U0 is incident on this step
from the left.
(a) Write down the appropriate solutions for the time-independent Schroedinger equation for this particle in the x < 0 region and in the x > 0
region.
(b) Apply the appropriate boundary conditions at x = 0 to match these
solutions.
(c) Derive expressions for the probabilities that the particle is reflected
and transmitted by the step.
Solution:
- Concepts:
Square potentials, the potential step
- Reasoning:
We are given a piecewise constant potential and are asked to find the
probability of reflection (R) and transmission (T ).
- Details of the calculation:
(a) Write the time-independent Schroedinger equation as
(∂2/∂x2)Φ(x) + k2Φ(x) = 0. E -
U = ħ2k2/(2m).
Let k1 = (2mE/ħ2)½, k2
= (2m(E - U0)/ħ2)½,
Then in region 1 (x < 0) Φ1(x) = A1exp(ik1x) + A1'exp(-ik1x)
and in region 2 (x > 0) Φ2(x) = A2exp(ik2x) + A1'exp(-ik2x)
are the most general solutions.
(b) Φ is continuous at x = 0. Therefore A1
+ A1' = A2
+ A2' .
∂Φ/∂x is continuous at x = 0. Therefore ik1A1
- ik1A1'
= ik2A2 - ik2A2' .
We have two equations and four unknowns. No unique solution exists. Let us
limit ourselves to particles approaching from the left being transmitted or
reflected at the barrier. Then A2' = 0. We can then solve for A1'/A1
and A2/A1. We find
A1'/A1 = (k1 - k2)/(k1 +
k2) and A2/A1 = 2k1/(k1 +
k2)
The ratios are real and positive, there is no phase shift upon reflection and
transmission.
(c) Our solutions in regions 1 and 2 are plane wave solutions. They are not
square integrable, and a proper normalization is not possible. Plane wave
solutions are useful in describing steady streams of particles. To evaluate the
probability of reflection and transmission for such beams, we compare the
reflected and transmitted flux with the incident flux. Let P(x) be the
probability density at x, let x0 be some point in region 1, and let x0'
be some point in region 2. We then have
incident flux ∝ v1Pi(x0), reflected flux ∝ v1Pr(x0),
transmitted flux ∝ v2Pt(x0').
The reflectance is R = v1Pr(x0)/(v1Pi(x0))
= |A1'/A1|2 = (k1 - k2)2/(k1
+ k2)2,
and the transmittance is T = v2Pt(x0')/(v1Pi(x0))
= (k2/k1)|A1'/A1|2 = (4k2k1)/(k1
+ k2)2.
We have R = 1 - (4k2k1)/(k1 + k2)2,
T = (4k2k1)/(k1 + k2)2,
R + T = 1.
Problem:
Consider a one-dimensional quantum-mechanical scattering problem, involving a
particle of mass m moving through a region with potential energy function
U(x) = U0, 0 ≤ x ≤ L, U(x) = 0 otherwise.
The particle moves from -∞ to +∞. Assume that its energy is chosen to be
exactly U0. Find the transmission and the
reflection probabilities.
Solution:
- Concepts:
This is a "square potential" problem. We solve HΦ(x)
= EΦ(x) in regions where U(x) is constant and apply boundary conditions.
- Reasoning:
Assume U(x) = U = constant in certain regions of space. In such a region
the Schroedinger equation yields (∂2/∂x2)Φ(x)
+ (2m/ħ2)(E - U)Φ(x) = 0.
Let E > U: (∂2/∂x2)Φ(x)
+ k2Φ(x)
= 0. E - U = ħ2k2/(2m).
The most general solution is Φ(x)
= Aexp(ikx) + A'exp(-ikx), with A and A' complex constants.
Let E < U: (∂2/∂x2)Φ(x)
- ρ2Φ(x)
= 0. U - E = h2ρ2/(2m).
The most general solution is Φ(x)
= Bexp(ρx)
+ B'exp(-ρx),
with B and B' complex constants.
Let E = U: (∂2/∂x2)Φ(x) = 0. Φ(x) = Cx
+ C', with C and C' complex constants.
- Details of the calculation:
At
a finite step the boundary conditions are that Φ(x)
and (∂/∂x)Φ(x)
are continuous.
Let x < 0, define region 1, 0 < x < L define region 2, and x > L define
region 3, and let
E = U0 = h2k2/(2m).
The most general solutions in regions 1, 2, and 3 are:
Φ1(x)
= A1exp(ikx) + A1'exp(-ikx), Φ2(x)
= A2x + A2', Φ3(x)
= A3exp(ikx)
Boundary conditions:
x
= 0: (1) A1 + A1' = A2', (2) ikA1
- ikA1' = A2
x = L: (3) A2L + A2'= A3exp(ikL), (4)
A2 = ikA3exp(ikL).
R = |A1'/A1|2,
T = |A3/A1|2.
From (1) and (2): A1
+ A1' = A2', A1 - A1' = A2/(ik),
A1 = ½(A2' + A2/(ik)), A1' =
½(A2' - A2/(ik)).
A1'/A1 = (A2'/A2 -
1/(ik))/(A2'/A2 + 1/(ik))
From (3) and (4): A2L
+ A2'= A2/(ik), A2'/A2 = 1/(ik)
- L.
A1'/A1 = -L/(2/(ik) - L) = Lk/(2i + Lk).
R = (Lk)2/(4 + (Lk)2). T = 1 - R = 4/(4 + (Lk)2).
Problem:
Let U(x) = 0 for x < 0, U(x) = U0 > 0 for 0 < x < a, and
U(x) = 0 for x > a. A particle of mass m and energy E > U0 is incident on this potential barrier. Find the
energies E for which resonances occur, i.e. for which the probability of
transmission is 1.
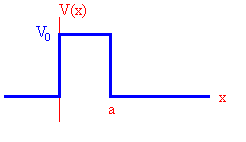
Solution:
- Concepts:
This is a "square potential" problem. We solve HΦ(x)
= EΦ(x) in regions where U(x) is constant and apply boundary conditions.
- Reasoning:
We are given a piecewise constant potential and are asked to find
the transmission coefficient T and the condition for T = 1.
- Details of the calculation:
The most general solutions in regions 1, 2, and 3 are
Φ1(x) = A1exp(ik1x) + A1'exp(-ik1x),
Φ2(x) = A2exp(ik2x) + A2'exp(-ik2x),
Φ3(x) = A3exp(ik1x).
Here k12 =
(2m/ħ2)E and k22 =
(2m/ħ2)(E - U0).
The boundary conditions are that
Φ(x) and (∂/∂x)Φ(x)
are continuous at x = 0 and x = a.
x = 0:
A1 + A1'
= A2 + A2' , ik1A1 - ik1A1'
= ik2A2 - ik2A2'.
x = a: A2exp(ik2a) + A2'exp(-ik2a)
= A3exp(ik1a),
ik2A2exp(ik2a) - ik2A2'exp(-ik2a)
= ik1A3exp(ik1a).
We need to solve these equations for A3 in terms of A1.
(i) Solve for A2 and A2' in terms of A3.
A2 = ½exp(i(k1-k2)a)(1 + k1/k2)A3
= C A3.
A2' = ½exp(i(k1+k2)a)(1 - k1/k2)A3
= C' A3.
(ii) Now solve for A1 in terms of A3.
2A1 = A2 + A2' + (k2/k1)(A2
- A2') = (C + C' + (k2/k1)(C - C'))A3.
A1 = ([-i(k12 + k22))/(2k1k2)]sink2a
+ cosk2a)exp(ik1a)A3.
T = |A3/A1|2 = 4k12k22/[(k12
+ k22)2sin2k2a + 4k12k22cos2k2a]
= 4k12k22/[(k12
- k22)2sin2k2a + 4k12k22].
T = 1 is sin2k2a = 0, k2a = nπ,
k22 =
(2m/ħ2)(E - U0) = n2π2/a2,
E = (ħ2/(2m))n2π2/a2
+ U0, n = 1, 2, ... .
Problem:
A plane wave representing an electron beam with energy E is
incident from the negative x direction onto a potential energy step described by
the function
U(x) = U2 for x < 0,
U(x) = U1 for 0 < x < a,
U(x) = 0 for x > a,
where U1 = π2ħ2/(8ma2),
E = 2U1, U1 < U2 < E.
Evaluate the transmittance T. For which value of U2
is T the largest?
Solution:
- Concepts:
Square potentials
- Reasoning:
We are given a piecewise
constant potential and are asked to find the transmission coefficient T.
- Details of the calculation:
The most general
solutions in regions 1, 2, and 3 are
Φ1(x) = A1exp(ik1x)
+ A1'exp(-ik1x),
Φ2(x) = A2exp(ik2x)
+ A2'exp(-ik2x),
Φ3(x) = A3exp(ik3x).
Here k12 = (2m/ħ2)(2U1
- U2) and k22 = (2m/ħ2)U1, k32
= (2m/ħ2)2U1.
The boundary conditions
are that Φ(x) and (∂/∂x)Φ(x) are continuous at x = 0 and x = a.
x = 0: A1 + A1' = A2 + A2'
, ik1A1 - ik1A1' = ik2A2
- ik2A2'.
x = a: A2exp(ik2a) + A2'exp(-ik2a)
= A3exp(ik3a),
ik2A2exp(ik2a) - ik2A2'exp(-ik2a)
= ik3A3exp(ik3a).
We need to solve these equations for A3 in terms of A1.
(i) Solve for A2 and A2' in terms of
A3.
A2 = ½exp(i(k3-k2)a)(1 + k3/k2)A3
= C A3.
A2' = ½exp(i(k3+k2)a)(1 - k3/k2)A3
= C' A3.(ii) Now solve for A1 in terms of A3.
2A1 = A2 + A2' + (k2/k1)(A2
- A2') = (C + C' + (k2/k1)(C - C'))A3.
C + C' = ½exp(i(k3a)[(2cos(k2a) - (k3/k2)2i
sin(k2a)]
C - C' = ½exp(i(k3a)[-2i sin(k2a)
+ (k3/k2) 2cos(k2a)]
C + C' + (k2/k1)(C - C') = exp(i(k3a)[(1 + k3/k1) cos(k2a) - i((k3/k2
+ k2/k1) sin(k2a)]
A1 = {[-i(k1k3 + k22))/(2k1k2)]sink2a
+ [(k1k2 + k3k2)/(2k1k2)]cosk2a}exp(ik1a)A3.
|A3/A1|2 = 4k12k22/[(k1k3
+ k22)2sin2k2a + (k1k2
+ k3k2)2(cos2k2a)]
In this problem since k22a2 = (2m/ħ2)U1a2
= π2/4, sin2k2a
= 1, cos2k2a = 0, k22 = ½k32.
|A3/A1|2 = 4k12k22/(k1k3
+ k22)2 = 2k12k32/(k1k3
+ ½k32)2 = 8/(2 + k3/k1)2.
T = (k3/k1)| |A3/A1|2
= 8(k3/k1) /(2 + k3/k1)2.
Let X = k3/k1, X2 = 2U1/(2U1
- U2), 2 < X2 < ∞, since U1 < U2
< 2U1.
T = 8X/(2 + X)2,
dT/dX = 0 --> 8(2
+ X) - 16X = 0, X = 2, X2 = 2U1/(2U1
- U2) = 4, U2 = 3U½.
T is largest for U2 = 3U½. Then T = 1.
Problem:
(a)
Calculate the transmission coefficient for a particle with mass m and kinetic
energy E passing through the rectangular potential barrier
U(x) = 0 for x < 0, U(x) = U0 for 0 < x < a, U(x) = 0 for x
> a, with E < U0.
(b) Show that for E << U0 and 2mU0a2/ħ2
>> 1 the transmittance T can be written as
T ~ (16E/U0)exp[-2(2m(U0
a2)/ħ2)½].
Solution:
- Concepts:
This is a "square potential" problem. We solve HΦ(x) = EΦ(x) in regions where
U(x) is constant and apply boundary conditions.
- Reasoning:
We are given a piecewise constant potential. We are asked to find the
transmission coefficient t.
- Details of the calculation:
Divide space into 3 regions; region 1: x' < 0, region 2: 0 < x' < a, region 3:
x' > a.
(a) potential barrier, E < U0.
The most general solutions in regions 1, 2, and 3 are
Φ1(x') = A1exp(ik1x') + A1'exp(-ik1x'),
Φ2(x') = A2exp(ρ2x') + A2'exp(-ρ2x'),
Φ3(x') = A3exp(ik1x').
Here k12 = (2m/ħ2)E and ρ22
= (2m/ħ2)(U0 - E).
The boundary conditions are that Φ(x') and (d/dx')Φ(x') are continuous at x' = 0
and x' = a.
x = 0: A1 + A1' = A2
+ A2' , ik1A1
- ik1A1' = ρ2A2 - ρ2A2'.
x = a: A2exp(ρ2a) + A2'exp(-ρ2a)
= A3exp(ik1a),
ρ2A2exp(ik2a) - ρ2A2'exp(-ρ2a) = ik1A3exp(ik1a).
We need to solve these equations for A3 in terms of A1.
(i) Solve for A2 and A2' in terms of A3.
A2 = ½ exp((ik1
- ρ 2)a)(1 + ik1/ρ 2)A3 = C A3.
A2' = ½ exp((ik1
+ ρ 2)a)(1 - ik1/ρ
2)A3 = C' A3.
(ii) Now solve for A1 in terms of A3.
2A1 = A2 + A2' + (ρ2/ik1)(A2
- A2') = (C + C' + (ρ2/ik1)(C - C'))A3.
A1 = [[(k12 - ρ22)/(2ik1ρ2)]sinhρ2a
+ coshρ2a ] exp(ik1a)A3.
t = A3/A1 = exp(-ik1a)/[[(k12
- ρ22)/(2ik1ρ2)]sinhρ2a +
coshρ2a]
T = |A3/A1|2 = 4k12ρ22/[(k12
- ρ22)2sinh2ρ2a + 4k12ρ22cosh2ρ2a]
= 4k12ρ22/[(k12
+ ρ22)2sinh2ρ2a + 4k12ρ22].
[cosh2x - sinh2x = 1.]
T = 4E(U0 - E) / [(U02sinh2[(2m(U0
- E)/ħ2)½
a] + 4E(U0 - E)].
(b) Let E << U0 and 2mU0a2/ħ2
>> 1.
sinh(x) = ½ (ex - e-x). If x >> 1 sinh(x) ~ ½ ex.
T ~ 4EU0/[(U0
2/4)exp[2(2m(U0 a2)/ħ2)½]
+ 4EU0 ] = 1/ [(U0/(16E))exp[2(2m(U0 a2)/ħ2)½
+ 1]
T ~ (16E/U0)exp[-2(2m(U0 a2)/ħ2)½].
Problem:
(a) Calculate the transmission coefficient for a particle with
mass m and kinetic energy E < U0 passing through the rectangular potential
barrier
U(x) = 0 for x < 0, U(x) = U0 > 0 for 0 < x < a, and
U(x) = 0 for x > a.
(b) Show that for E << U0 and 2mU0a2/ħ2
>> 1 the transmission coefficient can be written as
T ≈ (16E/U0)exp[-2(2mU0/ħ2)½a].
(c) Many heavy nuclei decay by emitting an alpha particle.
In a
simple one-dimensional model, the potential barrier the alpha particles have to penetrate
can be approximated by
U(r) = 0 for r < R0, U(r)
= U0R0/r for r > R0,
where R0 is the radius of the nucleus and
U0 is the
barrier height for r0 = R. The energy E of the alpha particle can
be assumed to be much smaller than U0. For a non constant potential
barrier the expression for the transmission coefficient found in part (b) can be used as a
guide. Assume that for E << U0, we have T ≈ exp[-2∫R1R2 dr (2m(U(r) - E)/ħ2)½].
The integration limits R1
and R2 are determined as solutions to the equation U(r) = E.
Calculate the alpha transmission coefficient and the decay constant λ,
i.e. the decay probability per second.
Solution:
- Concepts:
This is a "square potential" problem. We solve HΦ(x)
= EΦ(x) in regions where U(x) is constant and
apply boundary conditions.
- Reasoning:
We are given a piecewise constant potential. We are asked to find the
transmittance T.
- Details of the calculation:
(a)
Divide space into 3 regions;
region 1: x < 0, region 2: 0 < x < a, region 3: x > a.
(a) potential barrier, E < U0.
The most general solutions in regions 1, 2, and 3 are
Φ1(x) = A1exp(ikx) + A1'exp(-ikx),
Φ2(x) = B2exp(ρx) + B2'exp(-ρx),
Φ3(x)
= A3exp(ikx).
Here k2 = (2m/ħ2)E and ρ2
= (2m/ħ2)(U0 - E).
The boundary conditions are that
Φ(x) and (∂/∂x)Φ(x)
are continuous at x = 0 and x = a.
x = 0: A1 + A1' = B2 + B2', ikA1 - ikA1' = ρB2
- ρB2'.
x = a: B2exp(ρa) + B2'exp(-ρa)
= A3exp(ika),
ρB2exp(ik2a) - ρB2'exp(-ρa)
= ikiA3exp(ika).
We need to solve these equations for A3 and A1' in terms of A1.
(i) Solve for B2 and B2' in terms of A3.
B2 = ½exp((ik - ρ)a)(1 + ik/ρ )A3
= C A3.
B2' = ½exp((ik + ρ)a)(1 - ik/ρ)A3
= C' A3.
(ii) Now solve for A1 in terms of A3 to find T.
2A1 = B2
+ B2' + (ρ/ik)(B2 - B2') = (C + C' + (ρ/ik) (C
- C'))A3.
A1 = ([(k2 - ρ2)/(2ikρ)]sinhρa
+ coshρa)exp(ika)A3.
T = |A3/A1|2
= 4k2ρ2/[(k2
- ρ2)2sinh2ρa + 4k2ρ2cosh2ρa]
= 4k2ρ2/[(k2
+ ρ2)2sinh2ρa + 4k2ρ2].
[cosh2x - sinh2x = 1.]
T = 4E(U0 - E)/[U02sinh2[(2m(U0
- E)/ħ2)½a] + 4E(U0 - E)].(b) E << U0 and 2mU0a2/ħ2
>> 1.
sinh(x) = ½(ex - e-x) ≈ ½ex, if x >> 1.
Therefore
T ≈ 4E(U0 - E)/[¼U02exp[2(2m(U0
- E)/ħ2)½a] + 4E(U0 - E)]
≈ 4EU0/[¼U02exp[2(2mU0/ħ2)½a] + 4EU0)]
≈ (16E/U0)exp[-2(2mU0/ħ2)½a].
(c) Assume that
T ≈ exp[-2∫R1R2 dr (2m(U(r) - E)/ħ2)½].
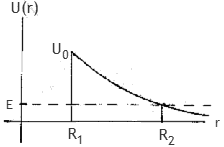
R1 = R0, R2 = U0R0/E,
R2 >> R1.
∫R1R2 dr (U(r) - E)½ = ∫R1R2 dr (U0R0/r
- U0R0/R2)½
= (U0R0)½∫R1R2 dr (1/r
- 1/R2)½.
∫R1R2 dr (1/r - 1/R2)½ = ∫R1R2 dr
[(R2 - r)/(rR2)]½
= √R2[(R1/R2 - (R1/R2)2)½
+ π/2 - tan-1(R1/(R2 - R1))½
--> √R2 π/2 if R2 >> R1.
T ≈ exp[-√(2m/E) πU0R0/ħ) = e-λ', λ' =
√(2m/E) πU0R0/ħ
e-λ' is the transmission coefficient.
To calculate the escape probability per second, we have to multiply T by the
rate of the alpha particle hitting the barrier, which is approximately v/R0.
escape probability ≈ √(2m/E)/R0 * e-λ' = λ =
1/τ.
This is a reasonable order of magnitude approximation as long as the escape
probability is very small.



