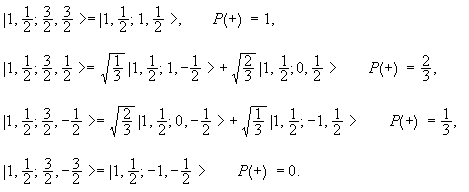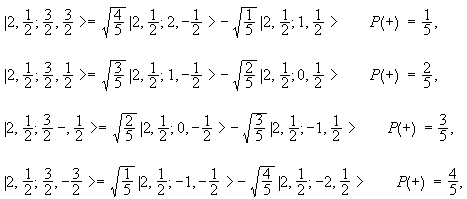Addition of angular momentum

Problem:

You have a system of two electrons whose orbital quantum numbers are l₁ = 2 and l₂ = 4 respectively.
(a)  Find the possible values of l (total orbital angular momentum quantum number) for the system.
(b)  Find the possible values of s (total spin angular momentum quantum number) for the system.
(c)  Find the possible values of j (total angular momentum quantum number) for the system

Solution:

• Concepts:
  Addition of angular momentum
• Reasoning:
  We are supposed to add the orbital and spin angular momentum.
• Details of the calculation:
  (a)  The quantum numbers associated with the total orbital angular momentum will range from a maximum value found by adding the individual quantum numbers together to a minimum value found by taking the absolute value of the difference of the two numbers in integer steps.
  l_max = l₁ + l₂ = 2 + 4 = 6
  l_min = |l₁ - l₂| = |2 - 4| = 2
  The possible values for L are 2, 3, 4, 5, and 6 .
  (b)  The quantum numbers associated with the total spin angular momentum will range from a maximum value found by adding the individual quantum numbers together to a minimum value found by taking the absolute value of the difference of the two numbers in integer steps.
  s_max = s₁ + s₂ = ½ + ½ = 1
  s_min = |s₁ - s₂| = |½ - ½| = 0
  The possible values for s are 0 and 1.
  (c)  The largest possible value for j will be found by adding together the maximum values for both l and s. The minimum value for j will be found by subtracting the largest possible value of s from the smallest possible value for l.
  j_smax = l_max + s_max = 6 + 1 = 7
  j_min = |l_min - s_max| = |2 - 1| = 1
  j = 1, 2, 3, 4, 5, 6, 7

Problem:

A hydrogen atom is known to be in a state characterized the quantum numbers n = 3, l = 2.
(a)    Give the allowed values of j.
(b)    For each of the allowed values of j, calculate the square of the magnitude of the total angular momentum.

Solution:

• Concepts:
  Addition of angular momentum
• Reasoning:
  We are supposed to add the orbital and spin angular momentum of the electron in the hydrogen atom.
• Details of the calculation:
  (a)  l = 2, s = ½, j = 5/2, 3/2.
  (b)  J²|jm> = j(j + 1)ħ²|jm>.
  For j = 5/2, j(j + 1)ħ² = (35/4)ħ².
  For j = 3/2, j(j + 1)ħ² = (15/4)ħ².

Problem:

Consider a deuterium atom (composed of a nucleus of spin 1 and an electron).  The electronic angular momentum is J = L + S, where L is the orbital angular momentum of the electron and S is its spin.  The total angular momentum of the atom is F = J + I, where I is the nuclear spin.  The eigenvalues of J² and F² are j(j + 1)ħ² and f(f + 1)ħ² respectively.
(a)  What are the possible values of the quantum numbers j and f for a deuterium atom in the 1s ground state?
(b)  What are the possible values of the quantum numbers j and f for a deuterium atom in the 2p excited state?

Solution:

• Concepts:
  Addition of angular momenta
• Reasoning:
  We are asked to add three angular momenta
• Details of the calculation:
  (a)  For the 1s ground state we have l = 0, J = L + S = S, j = ½.
  F = J + I, i = 1.
  The possible values for f are f = i + j, i - j;  f = 3/2, ½.
  (b)   For the 2p state we have l = 1.
  The possible values for j are j = l + s, l - s;  j = 3/2, ½.
  If j = 3/2 then the possible values for f are
  f = j + i, j + i - 1, j - i;  f = 5/2, 3/2, ½.
  If j = ½ then the possible values for f are
  f = i + j, i - j;  f = 3/2, ½.
  So the possible values for f are f = 5/2, 3/2, ½.

Problem:

We are to add two angular momenta characterized by the quantum numbers j₁ = 2 and j₂ = 1.
(a)  What are the possible values for j?
(b)  Express all eigenkets |j₁, j₂; j, m> = |2, 1; 1, m>  in terms of  |j₁, j₂; m₁, m₂>.
(c)  Express the ket  |j₁, j₂; m₁, m₂> =|2, 1; 0, 0> in terms of  |j₁, j₂; j, m>.
(d)  What are the expectation values of J_1z and J_2z in the state |j₁, j₂; j, m> = |2, 1; 1, 1>?

Solution:

• Concepts:
  Addition of angular momentum, the Clebsch-Gordan coefficients
• Reasoning:
  Consider two angular momentum operators J₁ and J₂.  J₁ operates in E₁ and J₂ operates in E₂. 
  Let J = J₁ +J₂.  J operates in E = E₁⊗E₂. 
  Since the operators J₁², J_1z , J₂², and J_2z all commute, a basis of common eigenvectors for E exists. 
  We denote this basis by {|j₁, j₂; m₁, m₂>}. 
  Since the operators J₁², J₂², J², and J_z all commute, a basis of common eigenvectors for E exists. 
  We denote this basis by {|j₁, j₂; j, m>}. 
  We can write the vectors of one basis as linear combinations of the vectors of the other basis.
  |j₁,j₂;j,m> = ∑_m1∑_m2 C^j_m1m2|j₁,j₂;m₁,m₂>,
  |j₁,j₂;m₁,m₂> = ∑_j∑_m C^j_m1m2|j₁,j₂;j,m>.
  The C^j_m1m2 = <j₁,j₂;m₁,m₂|j₁,j₂;j,m> are called the Clebsch-Gordon coefficients.
• Details of the calculation:
  (a)  |j₁ - j₂| ≤ j ≤ j₁ + j₂.  j = 3, 2, 1.
  (b) |j₁, j₂; j, m>
  Using a table of Clebsch-Gordan coefficients we find:
  |2, 1; 1, 1> = (3/5)^½|2, 1; 2, -1> - (3/10)^½|2, 1; 1, 0> + (1/10)^½|2, 1; 0, 1>
  |2, 1; 1, 0> = (3/10)^½|2,1;1 ,-1> - (2/5)^½|2, 1; 0, 0> + (3/10)^½|2, 1; -1, 1>
  |2, 1; 1, -1> = (1/10)^½|2,1;0,-1> - (3/10)^½|2, 1; -1, 0> + (3/5)^½|2, 1; -2, 1>
  (c) |j₁, j₂; m₁, m₂>
  Using a table of Clebsch-Gordan coefficients we find:
  |2, 1; 0, 0> = (3/5)^½|2, 1; 3, 0> - (2/5)^½|2, 1; 1, 0>
  (d)  Using the result from part (b) we have
  <J_1z> = 2ħ(3/5) + ħ(3/10) = 3ħ/2,
  <J_2z> = -ħ(3/5) + ħ(1/10) = -ħ/2.

Problem:

A particle of spin 3/2, at rest in the laboratory, disintegrates into two particles, one of spin ½ and one of spin 0.
(a)  What values are possible for the relative orbital angular momentum of the two particles?  Show that there is only one possible value if the parity of the relative orbital state is fixed.
(b)  Assume the decaying particle is initially in the eigenstate of S_z with eigenvalue mħ.  Is it possible to determine the parity of the final state by measuring the probabilities of finding the spin ½ particle either in the |+> or |-> state?

Solution:

• Concepts:
  Conservation of angular momentum, addition of angular momentum, the Clebsch-Gordan coefficients, orbital angular momentum and parity
• Reasoning:
  The total angular momentum of an isolated system is conserved.  The initial state has only spin angular momentum. The spin angular momenta and the orbital angular momentum of the particles in the final state must add to give the angular momentum of the initial state.

• Details of the calculation:
  (a)  The initial value of j is j = 3/2. We need the final value to be j = 3/2, since angular momentum of an isolated system is conserved.  Let us call the initial particle particle a, the spin ½ particle particle b, and the spin 0 particle particle c.  Then the total spin of the two particles in the final state is S = S_b + S_c = S_b.  Therefore the spin quantum number is s = ½. The possible values for the orbital angular momentum quantum number are l = 1 and l = 2.
  (j = l + s, ..., l - s; j = l + ½, l - ½, implies l = 1 or l = 2.)  The parity of the orbital state is (-1)^l.  If the parity is odd, we have l = 1, if the parity is even, we have l = 2.
  (b)  Assume that the final state has l = 1.
  It may be written as |j₁, j₂; j, m> = |1, ½; 3/2, m>.
  We may write it as a linear combination of |j₁, j₂; m₁, m₂> = |1, ½; m_l, m_s >.
  m can take on the values 3/2, ½, -½, -3/2.  Using a table of Clebsch-Gordan coefficients we find

  

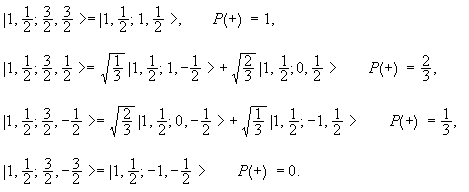
  Here P(+) is the probabilities of finding the spin ½ particle in the |+> state.

  Now assume that the final state has l = 2.
  It may be written as |j₁, j₂; j, m> = |2, ½; 3/2, m>.
  We may write it as a linear combination of |j₁, j₂; m₁, m₂> = |2, ½; m_l, m_s >.
  m can take on the values 3/2, ½, -½, -3/2.  We find

  

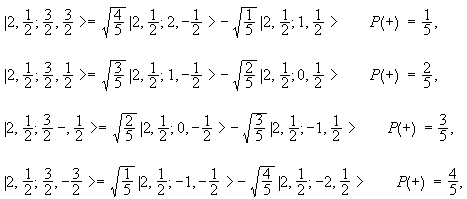
  Yes, it is possible to determine the parity of the final state by measuring the probabilities of finding the spin ½ particle either in the |+> or |-> state.