Orbital angular momentum
Problem:
Consider a spinless particle
of mass m. What values can the magnitude of the angular momentum J take in
quantum mechanics when it is measured?
Solution:
- Concepts:
Orbital angular momentum in QM
- Reasoning:
The only type of angular momentum for this
particle is orbital angular momentum.
- Details of the calculation:
When measuring L2 we only can
obtain an eigenvalue l(l +1)ħ2,
with l a non-negative integer.
The magnitude of the angular momentum J therefore can only be measured as
J = (l(l +1))½ħ,
l = 0, 1, 2, ... .
Problem:
The magnitude of the orbital angular momentum
L of a
hydrogen atom is found to be 30½ħ. Lz is measured and
found to be 3ħ.
(a) Which values of the principle quantum number n are consistent with these
measurements?
(b) What is the value of Lx2 + Ly2?
Solution:
- Concepts:
Angular momentum, the hydrogen atom
- Reasoning:
For the hydrogen atom H, L2 and Lz are commuting
observables.
- Details of the calculation:
(a) L2 = l(l+1)ħ2 = 30ħ2,
l
= 5. For the hydrogen atom the allowed value for l are all non-negative
integers equal to or less than n - 1. So n must be a positive integer greater or
equal to 6.
(b) Lx2 + Ly2 = L2 - Lz2
= (30 - 9)ħ2 = 21ħ2.
Problem:
A given normalized wave function is ψ(θ,φ) = N sinθ cosφ.
(a) Write this wave function in terms of spherical harmonics.
(b) Find the normalization constant N.
(c) What is the mean value of L2 for a state
with this wave function?
(d) Lz is measured. What are the possible results of this
measurement and what are the respective probabilities?
Solution:
- Concepts:
The spherical harmonics, the postulates of quantum
mechanics
- Reasoning:
If we want to find the probability of measuring the
eigenvalue a of an observable A we must express the wave function of the
system as a linear combination of eigenfunctions of A. Then P(a) = Σi|<ai|ψ>|2.
- Details of the calculation:
Express the wave function in terms of
spherical harmonics.
(a)
cosφ = ½(exp(iφ) + exp(-iφ)).
ψ(θ,φ) = -(N/2)(8π/3)½Y11 + (N/2)(8π/3)½Y1-1.
(b)
∫0πsinθ
dθ∫02πdφ Y*l'm'(θ,φ)Ylm(θ,φ)
= δl'lδm'm.
1 = (N2/2)(8π/3). N2 = 2/(8π/3)½.
ψ(θ,φ) = 2½Y1-1 - 2-½/Y11.
(c)
The given wave function is an eigenfuction of L2 with eigenvalue 2ħ2.
(d)
The possible results of measuring Lz are ħ and -ħ. The
probability of obtaining each of these results is ½.
Problem:
Show that a state with position wave
function (y - iz)k is an eigenstate of the orbital angular momentum
operator Lx and find its eigenvalue. Are there conditions on k?
Solution:
- Concepts:
Eigenfunctions, orbital angular momentum operators
- Reasoning:
The orbital angular momentum operator in Cartesian coordinate has the form
L = r ×
p.
We check if (y - iz)k is an
eigenfunction of Lx = ypz - zpy = (ħ/i)(y∂/∂z
- z∂/∂y).
- Details of the calculation:
∂(y - iz)k/∂z = -k*(y - iz)k-1*i,
∂(y - iz)k/∂y = k*(y - iz)k-1.
Lx(y - iz)k = (ħ/i)(-iky - kz) (y - iz)k-1
= -ħk(y - iz)k. The eigenvalue is -ħk.
k must be an integer.
Problem:
For a simple particle moving in space, show that the wave function ψlm(r) = x2 + y2
- 2z2 represents a simultaneous eigenstate of L2 and Lz
with eigenvalues l(l + 1)ħ2
and mħ. Determine l and m. Find a
function with the same eigenvalue for L2 and the maximum possible
eigenvalue for Lz.
Solution:
- Concepts:
The eigenfunctions of the orbital angular momentum operator, the spherical
harmonics
- Reasoning:
The common eigenfunctions of L2 and Lz are the
spherical harmonics. We have to write the given wave functions in terms of the
spherical harmonics.
-
Details of the calculation:
ψlm(r) = x2 + y2
- 2z2 =
r2sin2θcos2φ
+ r2sin2θsin2φ
- 2r2cos2θ = r2(sin2θ
- 2cos2θ)
in spherical coordinates.
Express ψlm(r) in terms of the
spherical harmonics.
ψlm(r) = r2(1
- cos2θ - 2cos2θ)
= r2(1 - 3cos2θ)
= -r2(16π/5)½Y20(θ,φ).
[Formulas for some of the spherical harmonics:
Y00 = (4π)-½, Y1±1 =
∓(3/8π)½sinθ
exp(±iφ), Y10 = (¾π)½cosθ,
Y2±2 = (15/32π)½sin2θ
exp(±i2φ), Y2±1 =
∓(15/8π)½sinθ
cosθ exp(±iφ),
Y20 = (5/16π)½(3cos2θ
- 1).]
ψlm(r) is an eigenfunction of Lz
with eigenvalue 0 and an eigenfunction of L2 with eigenvalue 6ħ2
(l = 2). For l = 2 the maximum possible eigenvalue of Lz is mħ
= 2ħ. The corresponding eigenfunction is
Cr2Y22(θ,φ) = Cr2(15/32π)½sin2θ
exp(i2φ).
Problem:
The wave function of a particle subjected to a spherically symmetric
potential U(r) is given by ψ(r) = (x + y - 3z)f(r).
(a) Is ψ an eigenfunction of L2? If so, what is its l
value? If not, what are the possible values of l we may obtain when L2
is measured?
(b) What are the probabilities for the particle to be found in various ml
states?
(c) Suppose it is known somehow that ψ(r) is an energy eigenfunction
with eigenvalue E. Indicate how we may find U(r).
Solution:
- Concepts:
The eigenfunctions of the orbital angular momentum operator, the spherical
harmonics
- Reasoning:
The common eigenfunctions of L2 and Lz are the
spherical harmonics. We have to write the given wave functions in terms of the
spherical harmonics.
- Details of the calculation:
ψ(r) = (x + y - 3z)f(r) = (rsinθcosφ
+ rsinθsinφ
- 3rcosθ)f(r)
= rf(r)(sinθcosφ
+ sinθsinφ
- 3cosθ)
= rf(r)(sinθ ½(eiφ + e-iφ) - i sinθ ½(eiφ -
e-iφ) - 3cosθ)
= rf(r)(sinθ ½eiφ (1 - i) + sinθ ½ e-iφ (1 + i) -
3cosθ)
= rf(r)(2-½exp(-iπ/2) sinθeiφ + 2-½exp(iπ/2)
sinθ e-iφ - 3cosθ).
Y1±1 =
∓(3/8π)½sinθ
exp(±iφ), Y10 = (¾π)½cosθ.
ψ(r) = rf(r)(-exp(-iπ/2)(4π/3)½Y11(θ,φ)
+ exp(iπ/2)(4π/3)½Y1-1(θ,φ) - (12π)½Y10(θ,φ))
= rf(r)2√π(-exp(-iπ/2)(1/3)½Y11(θ,φ) + exp(iπ/2)(1/3)½Y1-1(θ,φ)
- (3π)½Y10(θ,φ))
= (44π/3)½rf(r)(-exp(-iπ/2)/11½Y11(θ,φ)
+ exp(iπ/2)/11½Y1-1(θ,φ) - 3/11½Y10(θ,φ))
= R(r) (-exp(-iπ/2)/11½Y11(θ,φ) + exp(iπ/2)/11½Y1-1(θ,φ)
- 3/11½Y10(θ,φ)).
The function of angle is normalized.
ψ(r) is an eigenfunction of L2 with eigenvalue
2ħ2, l = 1.
(b) The possible values of ml are 1, 0, -1.
P(ml = 1) = 1/11,
P(ml = -1) = 1/11,
P(ml = 0) = 9/11.
(c) The wave function ψklm(r,θ,φ)
= Rkl(r)Ylm(θ,φ) = [ukl(r)/r]Ylm(θ,φ)
is a product of a radial function Rkl(r) and the spherical harmonic Ylm(θ,φ).
The differential equation for ukl(r) is
[-(ħ2/(2m))(∂2/∂r2)
+ ħ2l(l+1)/(2mr2)
+ U(r)]ukl(r) = Eklukl(r).
Since ukl(r), Ekl and l are known, we can solve this
equation for U(r).
Problem:
The ladder operator L+ is given by
L+ = ħ exp(iφ) [∂/∂θ + i cotθ ∂/∂φ].
The spherical harmonics are given by
Ylm(θ,φ)
= Flm(θ)exp(imφ).
(a)
Show that
Yll(θ,φ)
= cl sinl(θ)exp(ilφ), where
cl is a constant.
(b) Indicate how you would proceed to find the
θ-dependence of Ylm(θ,φ).
Solution:
- Concepts:
The raising and lowering
operators L+ = Lx + iLy
and L- = Lx - iLy,
the general properties of angular momentum operators
- Reasoning:
L±|k,l,m>
= [l(l+1) - m(m±1)]½ħ|k,l,m±1>.
Since
LzYlm(θ,φ) = mħYlm(θ,φ), (ħ/i)(∂/∂φ)Ylm(θ,φ)
= mħYlm(θ,φ),
we separate variables and look for solutions of the form Ylm(θ,φ)
= Flm(θ)exp(imφ).
Wave functions must be
continuous at all points in space.
We therefore need
Ylm(θ,0)
= Ylm(θ,2π) or exp(im2π) = 1 or m = integer.
Since L+Yll(θ,φ)
= 0, we can find a differential equation satisfied
Fll(θ)
and solve it.
-
Details of the calculation:
(a)
L+Yll(θ,φ) = ħ exp(iφ) [∂/∂θ + i cotθ ∂/∂φ]Yll(θ,φ)
= 0
from the general theory.
[d/dθ + l cotθ]Fll(θ) = 0.
dFll(θ) = l cotθ dθ Fll(θ), dFll(θ)
= l Fll(θ) d(sinθ)/sinθ.
dFll(θ)/Fll(θ) = l d(sinθ)/sinθ = l
d(ln(sinθ)) = d(ln(sinθ))l = d(sinθ)l/(sinθ)l
--> Fll(θ) = cl(sinθ)l.
Yll(θ,φ)
= cl
sinl(θ)exp(ilφ). Yll
is uniquely defined up to the arbitrary constant cl.
∫0πsinθ
dθ∫02πdφ |Ylm(θ,φ)|2
= |cl|2∫0πsinθ
dθ∫02πdφ
sin2l(θ) = 1
determines |cl| = (1/(2ll!))((2l+1)!/(4π))½.
It is customary to choose the phase of cl such that
|cl| = [(-1)l/(2ll!)] ((2l+1)!/(4π))½.
Yll(θ,φ)
is thus uniquely determined.
(b) L-|k,l,m>
= [l(l+1) - m(m±1)]½ħ|k,l,m-1>
from the general theory.
L-l-m|k,l,l> ∝
|k,l,m>.
L- is a differential operator. Apply it (l - m) times to Yll(θ,φ)
to obtain an expression for Ylm(θ,φ).
The
Ylm(θ,φ)
are thus uniquely defined.
To each pair (l,m) there corresponds one and
only one eigenfunction Ylm(θ,φ).
Problem:
A particle in a spherical potential is known to be in an eigenstate of L2
and Lz with eigenvalues l(l + 1)ħ2 and mħ, respectively.
Prove that the expectation values between |l m> states satisfy
<Lx> = <Ly> = 0, <Lx2> = <Ly2>
= (l(l + 1)ħ2 - m2ħ2)/2.
Solution:
- Concepts:
The raising and lowering operators L+ = Lx + iLy
and L+ = Lx - iLy,
L ±|k,l,m>
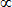 |k,l,m ± 1> follows from the commutation relations defining angular momentum.
|k,l,m ± 1> follows from the commutation relations defining angular momentum.
- Reasoning:
We can express Lx and Ly in terms of L+ and
L- and then find the matrix elements in the common eigenbasis of
L2 and Lz.
- Details of the calculation:
Lx = ½(L+ + L-) and Ly = (-i/2)(L+
- L-).
L ±|k,l,m>
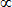 |k,l,m ± 1>, <k,l,m|L ±|k,l,m> = 0.
|k,l,m ± 1>, <k,l,m|L ±|k,l,m> = 0.
Therefore <Lx> = <Ly>
= 0.
Eigenstates of L2 and Lz have azimuthal symmetry.
This symmetry requires that <Lx2> = <Ly2>
= ½<Lx2
+ Ly2> = ½<L2 - Lz2>.
<Lx2> = <Ly2> = (l(l + 1)ħ2
- m2ħ2)/2.
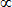 |k,l,m ± 1> follows from the commutation relations defining angular momentum.
|k,l,m ± 1> follows from the commutation relations defining angular momentum.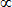 |k,l,m ± 1>, <k,l,m|L ±|k,l,m> = 0.
|k,l,m ± 1>, <k,l,m|L ±|k,l,m> = 0.