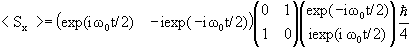A single spin ½ particle

Problem:

Explain why, in a Stern-Gerlach (SG) apparatus, a beam consisting of neutral particles in different spin states is split into different beams.

Solution:

• Concepts:
  The Stern-Gerlach experiment
• Reasoning:
  We are asked to explain the physics that determines the outcome af a Stern-Gerlach type experiment.
• Details of the calculation:
  If the neutral atoms have nonzero angular momentum J, they have a nonzero magnetic moment m = -(gμ_B/ħ)J.  In an external magnetic field a magnetic moment can experience a force and a torque.  The torque tries to align the magnetic moment with the magnetic field.  The force tries to pull an aligned dipole into regions where the magnitude of the magnetic field is larger and push an anti-aligned dipole into regions where magnitude the magnetic field is smaller.  If the magnetic field is pointing into the z-direction, the force on a magnetic dipole in that field is given by F_z = μ_z dB_z/dz.
  Angular momentum is quantized.  The possible values that we can measure for the square of the magnitude of the angular momentum are J² = j(j+1)ħ².  The possible projections we can measure along any axis, for example the z-axis, are J_z = mħ.  Here j is a non-negative integer or half integer, and for a given j, m can take on values from -j to j in integer steps.  Since J_z is quantized, μ_z is quantized, μ_z = -gμ_Bm.   If we passed a beam of randomly oriented atoms with angular momentum J through an inhomogeneous magnetic field, we would expect different atoms to be deflected by different discrete amounts depending on the quantized value of μ_z.

Problem:

An electron is in a state with z-component of spin angular momentum ħ/2.  An observation designed to measure the component of spin angular momentum along an arbitrary direction n is made.  What is the probability of observing a component of spin angular momentum ħ/2 along n?

Solution:

• Concepts:
  The two dimensional state space of a spin ½ particle, the postulates of quantum mechanics
• Reasoning:
  The electron is a spin ½ particle. The state space corresponding to the observable S_z of a spin ½ particle is two-dimensional.  We denote the eigenvectors of S_z by |+> and |->.  The matrix of S_z in the {|+>, |->} basis is
  .
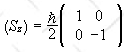  The matrices of S_x and S_y in the eigenbasis of S_z , {|+>, |->}, are not diagonal.

  , .
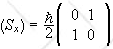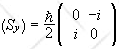  If n = n(θ,φ),  then the operator S_n defined through
  S∙n = S_xsinθcosφ + S_ysinθsinφ + S_zcosθ.
  The matrix of S_n is given in terms of the matrices of S_x, S_y, and S_z. 
  We can diagonalize it and find its eigenvectors |+>_n and |->_n. 
  The probability of observing a component of spin angular momentum ħ/2 along n is P = |_n<+|+>|².

• Details of the calculation:
  The matrix of S_n is
  (S_n) = (S_x)sinθcosφ + (S_y)sinθsinφ + (S_z)cosθ
  = .
  
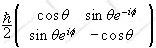  The eigenvectors of S_n are
  |+>_n = cos(θ/2)exp(-iφ/2)|+> + sin(θ/2)exp(iφ/2)|->,
  |->_n = -sin(θ/2)exp(-iφ/2)|+> + cos(θ/2)exp(iφ/2)|->.
  The probability of observing a component of spin angular momentum ħ/2 along n is
  P = |_n<+|+>|² = cos²(θ/2).

Problem:

A beam of electrons in an eigenstate of S_z with eigenvalue ½ħ is fed into a Stern-Gerlach apparatus, which measures the component of spin along an axis at an angle θ to the z-axis and separates the particles into distinct beams according to the value of this component.  Find the ratio of the intensities of the emerging beams.

Solution:

• Concepts:
  The two dimensional state space of a spin ½ particle, the postulates of quantum mechanics
• Reasoning:
  The electron is a spin ½ particle. The state space corresponding to the observable S_z of a spin ½ particle is two-dimensional.  It can be spanned by the eigenstates of S_z by {|+>, |->} or the eigenstates of S_n by {|+>_n, |->_n}.
  If n = n(θ,φ),  then the operator S_n defined through
  S∙n = S_xsinθcosφ + S_ysinθsinφ + S_zcosθ.
• Details of the calculation:
  The eigenvectors of S_n are
  |+>_n = cos(θ/2)exp(-iφ/2)|+> + sin(θ/2)exp(iφ/2)|->,
  |->_n = -sin(θ/2)exp(-iφ/2)|+> + cos(θ/2)exp(iφ/2)|->,
  or
  |+> = cos(θ/2)|+>_n - sin(θ/2)|->_n, 
  |-> = sin(θ/2)|+>_n + cos(θ/2)|->_n.
  At t = 0 the system is in the state |+>.  The Hamiltonian is proportional to S_n.  We want to find the probabilities of finding the system in the states |+>_n and |->_n.
  P(|+>_n) = |_n<+|+>|² = cos²(θ/2).
  P(|->_n) = |_n<-|+>|² = sin²(θ/2).
  The ratio of the intensities of the emerging beams is
  P(|+>_n)/P(|->_n)  = cot²(θ/2).

Problem:

Consider a beam of N silver atoms per second in their ground state.  The atoms are polarized in the |+> state, (i.e. the spin-up state of S_z), and travel along the y-axis with a constant velocity of magnitude v₀. 
The atoms traverse a region of space of length L which contains a uniform static magnetic field of strength B, directed along the y-axis, i.e. the direction of travel.
Note:  The translational motion of the center of mass of the atoms is treated classically.
(a)  Upon leaving the region of length L, the atoms enter a spin analyzer (a Stern-Gerlach device) with its magnetic field directed along the positive z-axis and the field gradient pointing in the -z direction.  What is the number of atoms per second in either of the beams emerging from the analyzer?

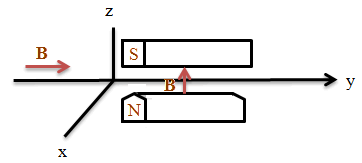
(b)  How should the analyzer be oriented, (i.e. what should be the direction of the magnetic field of the analyzer), so that only one beam emerges from the analyzer?   Interpret this result physically.

Recall that the spin gyromagnetic factor for the electron is given by γ = 2μ_B/ħ, where μ_B = q_eħ/(2m_e) is the Bohr magneton.  For the electron μ = -γS. 

Solution:

• Concepts:
  The two dimensional state space of a spin ½ particle, the evolution operator, the postulates of Quantum Mechanics
• Reasoning:
  Each atom has a magnetic moment μ = γS.  In a magnetic field B the Hamiltonian of an atom is H = -μ∙B = -γS∙B.
  The initial state evolves as |ψ(t)> = exp(-iHt/ħ)|ψ(0)>.
• Details of the calculation:
  (a)  Assume an atom enters the field region in the state |+>.   It leaves the field region after a time interval Δt = L/v₀.  During this time interval the Hamiltonian is -γBS_y = ω₀S_y.
  |ψ(L/v₀)> = exp(-iω₀S_yΔt/ħ)|+> = exp(-iω₀S_yΔt/ħ) (1/√2)(|+>_y + |->_y).
  |±>_y = (1/√2)(|+> ± i|->),  |±> = (1/√2)(|+>_y ± |->_y).
  S_y|±>_y = ±ħ/2)|±>_y.
  |ψ(L/v₀)> = (1/√2)(exp(-iω₀L/(2v₀))|+>_y + exp(iω₀L/(2v₀))|->_y)
  = ½(exp(-iω₀L/(2v₀))(|+> + i|->) + exp(iω₀L/(2v₀))(|+> - i|->))
  = cos(ω₀L/(2v₀))|+> + sin(ω₀L/(2v₀))|->.
  Now the atom enters a spin analyzer and are acted on by a force F_z = μ_zdB_z/dz.
  Atoms in the |+> state are deflected in the +z direction (μ_z and dB_z/dz are both negative) and atoms in the |-> state are deflected in the -z direction.
  The number of atoms leaving the analyzer in the |+> state is N₊ = N cos²(ω₀L/(2v₀) and the number of atoms/s leaving the analyzer in the |-> state is N_- = N sin²(ω₀L/(2v₀).
  N₊ + N_- = N.
  
  (b)  We need to rotate the apparatus about the y-axis so it makes an angle θ with the z-axis.
  Assume the spin analyzer is oriented so it deflects atoms in the |+>_n state in the n(θ,0) direction.
  |+>_n = cos(θ/2)|+> + sin(θ/2)|->,
  |->_n = -sin(θ/2)|+> + cos(θ/2)|->.
  |ψ(L/v₀)> = cos(ω₀L/(2v₀))|+> + sin(ω₀L/(2v₀))|->. 
  For all atoms to exit in the |+>_n state we need ω₀L/v₀ = θ + n2π,  n = integer.
  For all atoms to exit in the |->_n state we need ω₀L/v₀ = θ - π + n2π, n = integer.
  
  Physically, the polarization axis of the beam precesses about the magnetic field direction with angular frequency ω₀.  After a time interval L/v₀ the precession stops, and if we rotate the spin analyzer by the same angle, all the atoms will be transmitted.

Problem:

(a)  Determine the normalization constant A.
(b)  Find the expectation values <S_x>, <S_y>, and <S_z>.
(c)  Find the root-mean-square deviations ΔS_x, ΔS_y, and ΔS_z.

Solution:

• Concepts:
  The mean value and the root mean square deviation of an observable
• Reasoning:
  The expression for the mean value of an observable A in the normalized state |Ψ> is
  <A> = <Ψ|A|Ψ>.  If |Ψ> is not normalized then < A> = <Ψ|A|Ψ>/<Ψ|Ψ>.
  The root mean square deviation ΔA characterizes the dispersion of the measurement around <A>.
  ΔA = (<(A - <A>²)>)^½ = (<A²> - <A>²))^½.
  Here the system is the 2-dimensional state space of a spin-½ particle, and the observables are the Cartesian components of its spin.
• Details of the calculation:
  (a)  Normalization:  < χ| χ> = |A|²(9 + 16) = 25 |A|² = 1.  A = 1/5.
  (b)  Expectation values:
  

  <S_x> = <χ|S_x|χ> = (ħ/50) 

  -3i

  4

  	0	1
  	1	0

  	3i
  	4

   = 0.

   

  
  

  <S_y> = <χ|S_y|χ> = (ħ/50) 

  -3i

  4

  	0	-i
  	i	0

  	3i
  	4

   = -12ħ/25.

   

  
  

  <S_z> = <χ|S_z|χ> = (ħ/50) 

  -3i

  4

  	1	0
  	0	-1

  	3i
  	4

   = -7ħ/50.

   

  
  (c)  Root-mean-square deviations:
  ΔS_i = (<S_i²> - <S_i>²)^½,
  S_x² = S_y² = S_z²  = (ħ²/4)I,
  <S_x²> = <S_y^2> = <S_z²> = ħ²/4,
  This yields ΔS_x = ħ/2,  ΔS_y = 7ħ/50, and  ΔS_z = 12ħ/25.

Problem:

Two states of a spin ½ particle are represented in the eigenbasis of S_z by
|ψ₁> = (1/√2)(|+> + i|->),  |ψ₂> = (1/√3)(-i|+> + √2|->).
(a)  Find their representation in the eigenbasis of S_y.
(b)  Find the amplitude <ψ₁|ψ₂> in the S_z basis and show that this amplitude remains unchanged when calculated in the S_y basis.  (Show your work.)
(c)  The Hamiltonian for the particle is H = ω₀S_z.  Find |ψ₁(t)>.  At what times t is |ψ₁(t)> an eigenvector of S_x?

Solution:

• Concepts:
  Change of representation, the evolution operator
• Reasoning:
  We are switching from the eigenbasis of S_z to the eigenbasis of S_y and verify that inner products do not depend on the choice of representation.
  We use the evolution operator to find the state of the system at time t and then check if it is an eigenvector of S_x.

• Details of the calculation:
  (a)  The eigenvectors of S_y are |+>_y = (1/√2)(|+> + i|->) and |->_y = (1/√2)(|+> - i|->).
  Therefore: |+> = (1/√2)(|+>_y + |->_y) and |-> = (-i/√2)(|+>_y - |->_y).
  |ψ₁> = |+>_y.
  |ψ₂> = (-i/√6)(|+>_y + |->_y) - (i/√3)(|+>_y - |->_y) = (-i)(0.986|+>_y + 0.169|->_y
  (b)  <ψ₁|ψ₂> = (1/√6)(-i<+|+> - i√2<-|->) = -i/√6 - i√3 = -i0.986 in the S_z basis.
  <ψ₁|ψ₂> = (-i/√6)(_y<+|+>_y) - (i/√3)(_y<+|+>_y) = -i/√6 - i√3 = -i0.986 in the S_y basis.
  (c)  |ψ₁(t)> = (1/√2)(exp(-iω₀t/2)|+> + iexp(iω₀t/2)|->).
  
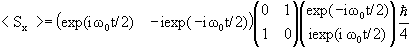
  = (ħ/4)i(-exp(-iω₀t) + exp(iω₀t)) = -(ħ/2)sin(ω₀t).
  If <S_x> = ±(ħ/2), then |ψ₁(t)> is an eigenvector of S_x.  This happens when ω₀t = nπ/2, n = odd.

Problem:

At t = 0 the x-component of the spin of a spin ½ particle is measured and found to be ħ/2.  At t = 0 the particle is therefore in the |+>_x eigenstate of the S_x operator.  The particle is confined to a region with a uniform magnetic field B = B₀k, its Hamiltonian is H = ω₀S_z.  The eigenstates of H are |+> and |->,
H|+> = (ħω₀/2)|+> and H|-> = -(ħω₀/2)|->.
|+>_x can be written as a linear combination of eigenstates of H.
(a)  Find the probability of measuring S_x = ħ/2 at t = T.
(b)  What is the mean value of S_x, <S_x>, at t = T?
(c)  Find the probability of measuring S_z = ħ/2 at t = T.

Solution:

• Concepts:
  The two dimensional state space of a spin ½ particle, the evolution operator, the postulates of Quantum Mechanics
• Reasoning:
  The state space corresponding to the observable S_z of a spin ½ particle is two-dimensional.  We denote the eigenvectors of S_z by |+> and |->.  The Hamiltonian of the system is H = ω₀S_z.  The evolution operator is exp(-iHt/ħ).  We use the evolution operator to find the state of the system at time T and then answer the questions using the postulates of Quantum Mechanics.
• Details of the calculation:
  (a)  The matrix of S_x in the eigenbasis of S_z is
  .
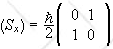  The eigenvectors of S_x are |+>_x and |->_x.
  |±>_x = (1/√2)(|+> ± |->).
  |ψ(t)> = U(t,0)|ψ(0)> = U(t,0)|+>_x = (1/√2)exp(-iHt/ħ)(|+> + |->).
  |ψ(t)> = (1/√2)(exp(-iω₀t/2)|+> + exp(iω₀t/2)|->).
  P(S_x=ħ/2,T) = |_x<+||ψ(t)>|² = ¼|(<+| + < -|)(exp(-iω₀T/2)|+> + exp(iω₀T/2)|->)|²
  = ¼|exp(-iω₀T/2)|+> + exp(iω₀T/2)|² = cos²(ω₀T/2).

  (b) P(S_x=-ħ/2,T) = 1 - cos²(ω₀T/2) = sin²(ω₀T/2).
  <S_x(T)> = (ħ/2)[cos²(ω₀T/2) - sin²(ω₀T/2)] = (ħ/2)cos(ω₀T).

  (c) P(S_z=ħ/2,T) = |<+|ψ(t)>|² = ½|<+|(exp(-iω₀t/2)|+>|² = ½.
  The probability of measuring S_z = ħ/2 is independent of t.

Problem:

An elementary spin-½ particle with magnetic moment μ_B is in it's lower level state in a magnetic field B parallel to z-axis.  At time t = 0 the magnetic field B is flipped to point parallel to x-axis.
(a)  Find the time-dependent spin wave function of the particle for t > 0.
(b)  Find the rotation frequency for the magnetic moment of the particle.

Solution:

• Concepts:
  The two dimensional state space of a spin ½ particle, the evolution operator, the postulates of Quantum Mechanics, the sudden approximation
• Reasoning:
  The state space corresponding to the observable S_x of a spin ½ particle is two-dimensional.  We denote the eigenvectors of S_x by |+>_x and |->_x.  After the magnetic field has suddenly been flipped the particle is not in an eigenstate of S_x, but in a linear combination of eigenstates. 
  |+> = 2^-½ (|+>_x + |->_x).
  The Hamiltonian of the system is H = ω₀S_x.  The evolution operator is exp(-iHt/ħ).  We use the evolution operator to find the state of the system at times t > 0, and then answer the questions using the postulates of Quantum Mechanics.
• Details of the calculation:
  (a)  Choose {|+> and |->}, the eigenstates of S_z, as the basis states.  Initially, these are the eigenstates of H.
  B = Bk.  H = -m∙B = -m_zB = -γS_zB = ω₀S_z.  Let ω₀ = -γB.
  At t = 0 the Hamiltonian becomes H = ω₀S_x and the eigenstates of the Hamiltonian become |+>_x and |->_x.
  |+> = 2^-½ (|+>_x + |->_x).
  |ψ(0)> = |+>.
  |ψ(t)> = U(t,0) |+> = 2^-½ U(t,0) (|+>_x + |->_x)
  = 2^-½ (exp(-iω₀t/2)|+>_x + exp(+iω₀t/2)|->_x)
  = 2^-1[exp(-iω₀t/2)(|+> + |->) + exp(+iω₀t/2)(|+> - |->)]
  = cos(ω₀t/2)|+> + isin(ω₀t/2)|->.
  (b)  P(S_z=ħ/2,t) = cos²(ω₀t/2),  P(S_z=-ħ/2,t) = sin²(ω₀t/2).
  <S_z>(t) = (ħ/2)( cos²(ω₀t/2) - sin²(ω₀t/2)) = (ħ/2)cos(ω₀t).
  The eigenvectors of S_y are |+>_y = (1/√2)(|+> + i|->) and |->_y = (1/√2)(|+> - i|->).
  <S_y>(t) = (ħ/2)|_y<+|ψ(t)>|² - (ħ/2)|_y<-|ψ(t)>|² =  (ħ/2)sin(ω₀t).
  <S_x>(t) = 0.
  We have Larmor precession with frequency |ω₀| about the x-axis.

Problem:

Consider a spin ½ particle with magnetic moment m = γS.  Let |+> and |-> denote the eigenvectors of S_z and let the state of the system at t = 0 be |ψ(0)> = |+>.
(a)  At t = 0 we measure S_y and find +½ħ.  What is the state vector |ψ(0)> immediately after the measurement?
(b)  Immediately after this measurement we apply a uniform, time-dependent field parallel to the z-axis.
The Hamiltonian operator becomes H(t) = ω₀(t)S_z.
Assume ω₀(t) = 0 for t < 0 and for t > T, and increases linearly from 0 to ω₀ when 0 < t < T.  Show that at time t the state vector can be written as
|ψ(t)> = 2^-½[exp(iθ(t))|+> + iexp(-iθ(t))|->]
and calculate the real function θ(t).
(c)  At time t = τ > T, we measure S_y.  What results can we find and with what probability? 
Determine the relation that must exist between ω₀ and T in order for us to be sure of the result.  Give a physical interpretation.

Solution:

• Concepts:
  The two dimensional state space of a spin ½ particle, the evolution operator, the postulates of Quantum Mechanics
• Reasoning:
  The state space corresponding to the observable S_z of a spin ½ particle is two-dimensional.  We denote the eigenvectors of S_z by |+> and |->.  The Hamiltonian of the system is H = ω₀(t)S_z.  We verify that the given |ψ(t)> is a solution to the Schroedinger equation and then answer the questions using the postulates of Quantum Mechanics.
• Details of the calculation:
  (a)  After the measurement |ψ(0)> = |+>_y = (1/√2)(|+> + i|->).
  (b)  Assume |ψ(t)> = 2^-½[exp(iθ(t))|+> + iexp(-iθ(t))|->].
  iħ∂|ψ(t)>/∂t = iħ2^-½[i (∂θ/∂t) exp(iθ(t))|+> + (∂θ/∂t) exp(-iθ(t))|->]
  = -ħ2^-½[(∂θ/∂t) exp(iθ(t))|+> - i(∂θ/∂t) exp(-iθ(t))|->].
  H|ψ(t)> = ω₀(t)S_z|ψ(t)> = 2^-½ω₀(t)(ħ/2)[exp(iθ(t))|+> - iexp(-iθ(t))|->].
  For ψ(t)> to be a solution to the Schroedinger equation we need ω₀(t)/2 = -∂θ/∂t,
  -dθ = ½ω₀(t)dt,  θ(t') - θ(0) = -½∫₀^t'ω₀(t)dt.
  θ(0) = θ(t < 0) = 0.   Let α = ω₀/T, then ω₀(t) = αT.
  θ(t') = -αt'²/4  for (0 < t' < T),  θ(t') = -αT²/4  for ( t' > T).
  (c)  |ψ(τ)> = 2^-½[exp(iθ(τ))|+> + iexp(-iθ(τ))|->].
  Possible result of measuring S_y are ±ħ/2.
  P(+ħ/2) = |_y<+|ψ(τ)>|² = ¼|exp(iθ(τ)) + exp(-iθ(τ)|² = cos²(θ(τ)).
  P(-ħ/2) = |_y<-|ψ(τ)>|² = sin²(θ(τ)).
  θ(τ) = -αT²/4.  We need  αT²/4 = nπ/2  or ω₀ = n2π/T  to be sure of the result.
  The physical interpretation is a precession, similar to Larmor precession.
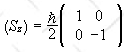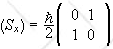
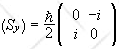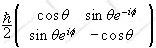