The hydrogen atom

Energy levels

Problem:

What is the ratio of the longest wavelength of the Balmer series to the longest wavelength of the Lyman series?

Solution:

• Concepts:
  The hydrogen atom
• Reasoning:
  hc/λ = 13.6 eV(1/n_f² - 1/n_i²)
  Longest wavelength  <-->  smallest energy difference
• Details of the calculation:
  For the Balmer series  hc/λ_max = 13.6 eV(¼ - 1/9)  (n = 3 --> n = 2).
  For the Lyman series:  hc/λ_max = 13.6 eV(1/1 - ¼)  (n = 2 --> n = 1).
  λ_max(Balmer)/λ_max(Lyman) = (1/1 - ¼) /(¼ - 1/9)  = 27/5.

Problem:

A hydrogen atom at rest in the laboratory emits the Lyman α radiation.
(a)  Express the measured wavelength in terms of the Rydberg constant R_H = 1.097*10⁷/m, which was determined from measurements.
(b)  Compute the recoil kinetic energy of the atom.
(c)  What fraction of the excitation energy of the n = 2 state is carried by recoiling atom.

Solution:

• Concepts:
  The hydrogen atom, momentum conservation
• Reasoning:
  The Rydberg constant was determined from measurements.  The measured wavelength of the photon is NOT the wavelength we calculate assuming a fixed atom.
• Details of the calculation:
  (a)  Lyman α radiation is produced in a n = 2 to n = 1 transition. 
  1/λ = R_H(1 - ¼) = 3R_H/4,  λ = 1.22*10^-7 m.
  The energy released in the transition is E = 13.6 eV(1 - ¼) = 10.2 eV.
  (b)  Momentum conservation requires that |p_photon| = |p_atom| = p,  h/λ = p.
  The recoil energy of the atom is p²/(2m) = (0.75 h R_H)²/(2m) = 8.9*10^-27 J = 5.58*10^-8 eV.
  (c)  The fraction of the excitation energy carried by the atom is 5.58*10^-8/10.2 = 5.5*10^-9.

Problem:

In the interstellar medium electrons may recombine with protons to form hydrogen atoms with high principal quantum numbers.  A transition between successive values of n gives rise to a recombination line.
(a)  A radio recombination line occurs at 5.425978 * 10¹⁰ Hz for a n = 50 to n = 49 transition.  Calculate the Rydberg constant for H.
(b)  Compute the frequency of the H recombination line corresponding to the transition n = 100 to n = 99.
(c)  Assume the mean speed in part (b) is 10⁶ m/s.  At what frequency or frequencies would the recombination line be observable?
(d)  Consider that radio recombination lines may be observed at either of two facilities, the 11 meter telescope at Kitt Peak near Tuscon, Arizona, and the 1.2 meter radio telescope at Columbia University in New York.  Relative larger blocks of time are available on the smaller telescope, but its intrinsic noise is moderately high.  Where would you choose to map recombination radiation emanating from an external galaxy.  Discuss both technical and non technical aspects of your choice.

Solution:

• Concepts:
  The hydrogen atom, transitions between energy levels, the Doppler shift
• Reasoning:
  The wavelengths of the light emitted by excited hydrogen atoms can be found using the formula
  1/λ = R_H(1/n² - 1/n'²).  The observed wavelengths depend on the relative speed of the source and the observer.

• Details of the calculation:
  (a)  E_n' - E_n = hν = hcR_H(1/n² - 1/n'²).
  5.425978 * 10¹⁰ = 2.99792458 * 10⁸R_H(¼9² - 1/50²),  R_H = 1.097373 * 10⁷ m^-1.
  (b)  ν = cR_H(1/99² - 1/100²) = 6.679710 * 10⁹ s^-1.
  (c)  The line is Doppler shifted.
  ν' = ν[(1 + v/c)/(1 - v/c)]^½ ~ ν(1 + v/c) if v/c << 1.
  Here v is the relative velocity of source and observer; v is positive if the source and the observer approach each other, and v is negative if the source and the receiver recede from each other.
  -10⁶/(3*10⁸) < v/c < 10⁶/(3*10⁸),   6.657 * 10⁹ s^-1 < ν' < 6.702 * 10⁹ s^-1.
  (d)  Here are some factors worth considering:
  The amount of radiation gathered by a telescope is proportional to the square of its diameter D.
  The smallest angle that can be resolved is approximately θ = λ/D.
  (For each photon we have ΔxΔp_x ~ h, Δx ~ D,  ΔP_x ~ h/D, θ = Δp_x/p = hc/(Dhν) = λ/D.)
  If you assume that the radiation has a frequency of ~ 10^-10 s^-1, then  λ = c/ν = 3 cm.  For the small telescope we therefore have θ = 0.03/1.2  while for the large telescope we have θ = 0.03/11.  It takes (11/1.2)² = 84 times as long to gather the same amount of radiation with the small telescope as with the large telescope.

Problem:

Determine the wavelengths of the first three transitions in the Balmer series for hydrogen.  How would the wavelengths change for an ion with Z = 2 (He⁺)?

Solution:

• Concepts:
  Hydrogenic atoms, The Balmer series
• Reasoning:
  Each time the energy level of the electron changes, a photon will be emitted and the energy (wavelength) of the photon will be characteristic of the energy difference between the initial and final energy levels of the atom in the transition. The lines for which n_f = 2 are called the Balmer series.
• Details of the calculation:
  The final state for a Balmer-series transition is n = 2.
  hf = -13.6 eV(1/n_i² - ½²) = 13.6 eV(¼ - 1/n_i²).
  We may write hc/λ = 13.6 eV(¼ - 1/n_i²)  or
  1/λ = (13.6 eV(/hc))(¼ - 1/n_i²) = R(¼ - 1/n_i²).
  R = 1.1*10^-2 nm^-1.
  n = 3 --> n = 2:  1/λ = (1.1*10^-2 nm^-1)(¼ - 1/9),  λ = 655 nm
  n = 4 --> n = 2:  1/λ = (1.1*10^-2 nm^-1)(¼ - 1/16),  λ = 485 nm
  n = 5 --> n = 2:  1/λ = (1.1*10^-2 nm^-1)(¼ - ½5),  λ = 433 nm
  Energy level and transition frequencies in hydrogenic atoms scale as Z², so for a  Z = 2 ion the transition wavelengths a factor of 4 smaller than those for hydrogen.

Problem:

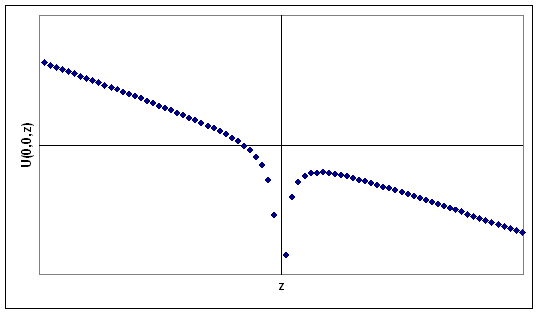
A hydrogen atom is placed in a uniform electric field, E = -Ek.  Place the proton at the origin of your coordinate system.  An electron in the hydrogen atom then has potential energy U(r) = -kq_e²/r - q_eEz.  U(0,0,z) becomes increasingly positive for negative z .  For positive z the potential energy U(0,0,z) contains a "hill" and then decreases with increasing z.
Sketch the potential energy of the electron, U(0,0,z), as function of z and calculate the energy at the maximum at positive z.  Equate this energy to the energy of the unperturbed (zero field) hydrogen energy level and thereby determine the value of the field required to field-ionize a hydrogen atom with principle quantum number n (neglect tunneling).

Solution:

• Concepts:
  The energy levels of the hydrogen atom
• Reasoning:
  The perturbed potential has a local maximum.  If an energy level of the unperturbed hydrogen atom lies above this local maximum, than field ionization is likely.
• Details of the calculation:
  
  U(0,0,z) = - kq_e²/|z| - q_eEz.
  For positive z:
  dU(0,0,z)/dz = kq_e²/z² - q_eE = 0.  z² = kq_e/E, z = (kq_e/E)^½.
  Let - kq_e²/(kq_e/E)^½ -  q_eE(kq_e/E)^½ = -(E_I)/n², with E_I = 13.6 eV.
  Then -2q_e(kq_eE)^½ = -(13.6 eV)/n²,  4kq_e³E = E_I²/n⁴,
  E = E_I²/(4kq_e³n⁴) = (3.21*10¹⁰ V/m)/n⁴.
  A reasonable field (kV/cm) can ionize levels with n > 24.

Wave functions

Problem:

An electron in the n = 2, l = 1, m = 0 state of a hydrogen atom has a wave function ψ(r,θ,φ) proportional to r exp(-r/(2a₀)) cosθ, where a₀ is the Bohr radius.
(a)  Find the normalized wave function ψ(r,θ,φ).
(b)  Find the probability per unit length of finding the electron a distance r from the nucleus.
(c)  Find the most probable distance R_MP of the electron from the nucleus.
(d)  Find the average distance <r> from the nucleus.

Solution:

• Concepts:
  The fundamental assumptions of Quantum Mechanics
• Reasoning:
  If the wave function is normalized, then |ψ(r,t)|² is the probability density.
  The expression for the mean value of any observable A in the normalized state |ψ> is
  <A> = <ψ|A|ψ>. 

• Details of the calculation:
  (a)  Normalization:
  ∫|ψ(r,θ,φ)|²d³r = 1,  ψ(r,θ,φ) = A r exp(-r/(2a₀)) cosθ.
  A²∫₀^2πdφ∫₀^πsinθ dθ∫₀^∞r²dr r²exp(-r/a₀) cos²θ
  = A²2π∫₀^πsinθ cos²θ dθ∫₀^∞r⁴dr exp(-r/a₀) = 1.
  A²2πa₀⁵∫_-1¹x²dx∫₀^∞r^'4dr' exp(-r') = A²2πa₀⁵(2/3)4!' = 1.
  A² = 1/(32πa₀⁵).
  ψ(r,θ,φ) = (32πa₀³)^-½(r/a₀) exp(-r/(2a₀)) cosθ.

  (b)  P(r,θ,φ)d³r = |ψ(r,θ,φ)|²d³r  is the probability of finding the electron in an infinitesimal volume d³r about r = (r,θ,φ). 
  P(r,θ,φ)  is the probability per unit volume.
  ∫₀^2πdφ∫₀^πsinθ dθ |ψ(r,θ,φ)|²r² = P(r).
  P(r) is the probability per unit length.
  P(r) =  [2π/(32πa₀⁵)] r⁴exp(-r/a₀)∫₀^πsinθ cos²θ dθ
  = [r⁴/(16a₀⁵)] exp(-r/a₀)(2/3) =  [r⁴/(24a₀⁵)] exp(-r/a₀).

  (c)   We are looking for the maximum in P(r).
  dP(r)/dr|_{(r = RMP)} = [1/(24a₀⁵)] [4r³ exp(-r/a₀) - (r⁴/a₀)exp(-r/a₀)]|_{(r = RMP)} = 0.
  R_MP = 4a₀.

  (d)   <r> = ∫₀^∞r P(r) dr = [1/(24a₀⁵)] ∫₀^∞r⁵ exp(-r/a₀) dr
  = [a₀/24] 5! = 5a₀.
  <r> > R_MP.

Problem:

Assume that the nucleus of a hydrogen atom is a sphere of radius b.  In the limit where
b << a₀ (where a₀ is the Bohr radius), what is the probability that an electron in the ground state of hydrogen will be found inside the nucleus?

Solution:

• Concepts:
  Ground-state wave function of the hydrogen atom
• Reasoning:
  The ground state wave function does not vary much over the volume of the nucleus, since b << a.
• Details of the calculation:
  The ground state wave function of the hydrogen atom is Φ₁₀₀(r) = (πa₀³)^-½ exp(-r/a₀).
  The probability of finding the electron inside the nucleus is
  P = V_n |Φ₁₀₀(0)|² = (4πb³/3) (πa₀³)^-1 = (4/3)(b/a₀)³.

Problem:

Find the momentum space wave function Φ(p) for the electron in the 1s state of the hydrogen atom.

Solution:

• Concepts:
  Change of representation, the Fourier transform
• Reasoning:
  We are asked to change from the r to the p representation.
  Φ(r) = (2πħ)^-3/2∫ d³p Φ(p)exp(ip∙r/ħ),
  Φ(p) = (2πħ)^-3/2∫d³r Φ(r)exp(-ip∙r/ħ).
  Φ(r) and Φ(p) are Fourier transforms of each other.
• Details of the calculation:
  The 1s wave function is
  Φ(r) = (πa₀³)^-½ exp(-r/a₀) = Φ(r).
  Symmetry demands that Φ(p) = Φ(p).
  Let us choose a convenient direction for p.  Let p = pk.  Then
  Φ(p) = (2πħ)^-3/2∫₀^2πdφ∫₀^πsinθ dθ∫₀^∞r²dr exp(-iprcosθ/ħ) (πa₀³)^-½exp(-r/a₀)
  = (2πħ)^-3/2(πa₀³)^-½2π∫_-1¹dcosθ∫₀^∞r²dr exp(-iprcosθ/ħ) exp(-r/a₀).
  
  ∫₀^∞r²dr exp(-iprcosθ/ħ) exp(-r/a₀) = 2/(iprcosθ/ħ + 1/a₀)³
  using ∫₀^∞xⁿ exp(-x) dx = n!.
  Φ(p) = a^-3/2ħ^3/2(√2)(-ip³π)^-1∫_-1¹dx (x + ħ/(ia₀p))^-3
  = (a₀ħ)^-3/2ħ³(√2)(-ip³π)^-1(2ħ/(ia₀p))(1 + ħ²/(a₀p)²)^-2.
  Φ(p) = (1/π) (2a₀/ħ)^3/2 [1/(1 + a₀²p²/ħ²)²] = Φ(p).

Problem:

The normalized wave function of an electron in a hydrogen atom, neglecting spin, is
ψ(r,t) = (1/3)^½Φ₁₀₀(r,θ,φ) + (2/3)^½Φ₂₁₀(r,θ,φ),
where the Φ_nlm(r,θ,φ) are the usual normalized hydrogenic eigenfunctions.
(a)  If a single measurement is made of the energy, what results are possible?
(b)  What are the probabilities of obtaining each of the particular possible results?
(c)  What is the expectation value of the energy?
(d)  If a single measurement is made of the total angular momentum, what results are possible?
(e)  What are the probabilities of obtaining each of the particular possible results?
(f)  If the observable O is a constant of the motion, then it satisfies the equation

d/dt<O> = <∂O/∂t> + (i/ħ)<[H,O]> = 0

where H is the Hamiltonian.
For the hydrogen atom described above, is the z-component of angular momentum, L_z, a constant of the motion?
(g)  Is the z-component of linear momentum, p_z, a constant of the motion?
(h)  How do the expectation values of L_z and p_z depend on time?

Given:
Φ₁₀₀(r,θ,φ) ∝ exp(-r/a₀),      Φ₂₁₀(r,θ,φ) ∝ (r/a₀) exp(-r/(2a₀)) cos(θ). 
∫Φ*₁₀₀ (∂/∂z) Φ₂₁₀ d³r  = (√2/a₀)(2/3)⁴ exp(-i(E₂ - E₁)t/ħ) = A exp(-i(E₂ - E₁)t/ħ)
∫Φ*₂₁₀ (∂/∂z) Φ₁₀₀ d³r  = -(√2/a₀)(2/3)⁴ exp(i(E₂ - E₁)t/ħ) = -A exp(i(E₂ - E₁)t/ħ)

Solution:

• Concepts:
  Postulates of Quantum Mechanics, the hydrogen atom
• Reasoning:
  The postulates of quantum mechanic contain the rules for making predictions about the outcome of measurements.
• Details of the calculation:
  (a)  The possible results are E₁ = -13.6 eV or E₂ = -13.6 eV/4 = -3.4 eV.
  (b)  P(E₁) = (1/3),  P(E₂) = (2/3).
  (c)  <E> = -13.6 eV/3 - 2*3.4eV/2 = 6.8.
  (d)  The possible results are  L = 0 or L = (2ħ²)^½.  (quantum number l = 0 or l = 1)
  (e)  P(L = 0) = (1/3),  P(L = 1.41ħ) = (2/3).
  (f)  H commutes with L_z.  ψ(r,t) is an eigenfunction of L_z with eigenvalue 0.  L_z is a constant of motion.
  (g)  H does not commute with p_z, p_z is not a constant of the motion.
  (h)  d<L_z>/dt = 0, since L_z is a constant of motion.
  <p_z> = (ħ/i) ∫ψ*(r,t)(∂/∂z)ψ(r,t)d³r
  = (ħ/i)[(1/3)∫Φ*₁₀₀(∂/∂z)Φ₁₀₀d³r + (2/3) ∫Φ*₂₁₀(∂/∂z)Φ₂₁₀d³r 
  + (√2/3) ∫Φ*₁₀₀(∂/∂z)Φ₂₁₀d³r  + (√2/3) ∫Φ*₂₁₀(∂/∂z)Φ₁₀₀d³r ]
  = (√2/3)(ħ/i)[A(exp(-i(E₂ - E₁)t/ħ) - A(exp(i(E₂ - E₁)t/ħ)] = (-2Aħ)(√2/3)sin((E₂ - E₁)t/ħ)
  [For any eigenstate of the hydrogen atom <p_z> = 0, therefore
  ∫Φ*₁₀₀(∂/∂z)Φ₁₀₀d³r  =  ∫Φ*₂₁₀(∂/∂z)Φ₂₁₀d³r  = 0.]

Problem:

For l = 2 in the hydrogen atom:
(a)  What is the minimum value of L_x² + L_y²?
(b)  What is the maximum value of L_x² + L_y²?
(c)  What is L_x² + L_y² for l = 2 and m_l = 1?  Can either L_x or L_y be determined from this?
(d)  What is the minimum value of n this state can have?

Solution:

• Concepts:
  Angular momentum, the hydrogen atom
• Reasoning:
  Φ_nlm(r) = R_nl(r)Y_lm(θ,φ) for hydrogen. 
  L²Y_lm(θ,φ) = l(l + 1)ħ²Y_lm(θ,φ),  L_zY_lm(θ,φ) = mħY_lm(θ,φ).
  The quantum number m can take up values from -l to l in integer steps.

• Details of the calculation:
  (a)  L² = L_x² + L_y² + L_z² =  l(l + 1)ħ² = 6ħ².  The maximum value of L_z is 2ħ, so the minimum value of L_x² + L_y² = L² - L_z² = 2ħ².
  (b) The minimum value of L_z is 0, so the maximum value of L_x² + L_y² = 6ħ².
  (c)  For l = 2 and m_l = 1 L_z² = ħ², so L_x² + L_y² = 5ħ².  Neither L_x or L_y can be determined from this?
  (d)  For the hydrogen atom the allowed value for l are all non-negative integers equal to or less than n - 1.  So the minimum value of n this state can have is 3.