Square potentials (cube and sphere)

Rectangular box

Problem:

An electron is trapped in a two-dimensional, infinite rectangular well of width L_x = 800 pm and L_y = 1200 pm.  What is the electron's ground state energy?

Solution:

• Concepts:
  The 1-D infinite square well
• Reasoning:
  We are asked to find the ground-state energy of an electron in an infinite square well.
• Details of the calculation:
  E = E_x + E_y.  E = n_x²π²ħ²/(2mL_x²)  + n_y²π²ħ²/(2mL_y²). 
  For the ground state n_x = n_y = 1, so E = π²ħ²/(2mL_x²)  + π²ħ²/(2mL_y²).
  E = [(π*1.05*10^-34)²/(2*9.1*10^-31*(800*10^-12)²) + (π*1.05*10^-34)²/(2*9.1*10^-31*(1200*10^-12)²] J
  = 1.22* 10^-19 J = 0.76 eU .

Problem:

Solve the time independent Schroedinger equation for the eigenfunctions and the corresponding energies of the infinite rectangular well (or "particle in a box") with sides a, b, c.  Do not just write down your answer but derive it.  Justify each step.

Solution:

• Concepts:
  The particle in a 3-dimensional box, separation of variables
• Reasoning:
  We are asked to find the eigenfunctions and eigenvalues of the Hamiltonian of a particle in a 3D box.
• Details of the calculation:
  Time independent Schroedinger equation:  (-ħ²/(2m))∇²Φ(r) + U(r)Φ(r)  = EΦ(r).
  Let us use Cartesian coordinates and choose the orientation and origin of the coordinate system such that
  U(x,y,z) = 0 if 0 < x < a AND 0 < y < b AND 0 < z < c,  U(x,y,z) = infinite otherwise.
  In Cartesian coordinate the 3D time-independent Schroedinger equation is 
  (-ħ²/(2m))[∂²Φ(x,y,z)/∂x² + ∂²Φ(x,y,z)/∂y² + ∂²Φ(x,y,z)/∂z²] + U(x,y,z)Φ(x,y,z)  = EΦ(x,y,z).

  We usually try to solve such equations by a technique called separation of variables.
  For a particle trapped in a rectangular "infinite well" the potential is 0 inside the well and infinite outside the well.  In the region where the potential is zero we solve the Schroedinger equation by trying a solution of the form Φ(x,y,z) = X(x)Y(y)Z(z).
  Then
  (-ħ²/(2m))[Y(y)Z(z)∂²X(x)/∂x² + X(x)Z(z) ∂²Y(y)/∂y² + X(x)Y(y)∂²Z(z)/∂z²]  = E X(x)Y(y)Z(z). 
  X(x)^-1∂² X(x)/∂x² + Y(y)^-1∂²Y(y)/∂y² + Z(z)^-1∂² Z(z)/∂z²  + (2m/ħ²)E = 0
  The first term is a function of x only, the second term is a function of y only, and the third term is a function of z only.  All three terms must be equal to constants and the sum of these constants must be equal to -(2m/ħ²)E.
  Write E = E_x + E_y + E_z.
  ∂²X(x)/∂x² + (2m/ħ²)E_xX(x) = 0.
  ∂²Y(y)/∂y² + (2m/ħ²)E_yY(y) = 0.
  ∂²Z(z)/∂z² + (2m/ħ²)E_zZ(z) = 0.
  The boundary conditions are
  X(x) = 0 at x = 0 and x = a.
  Y(y) = 0 at y = 0 and y = b.
  Z(z) = 0 at z = 0 and z = c.

  The normalized solutions to the differential equations are
  X(x) = (2/a)^½sin(n_xπx/a),  Y(y) = (2/b)^½sin(n_yπy/b),  Z(z) = (2/c)^½sin(n_zπz/c),
  n_x = 1, 2, 3, ...  ,  n_y = 1, 2, 3, ...  ,  n_z = 1, 2, 3, ...  . 
  E_nx = n_x²π²ħ²/(2ma²),  E_ny = n_y²π²ħ²/(2mb²),  E_nz = n_z²π²ħ²/(2mc²).

  The eigenfunctions for the problem therefore are
  Φ_nx,ny,nz(x,y,z) = (8/(abc))^½sin(n_xπx/a) sin(n_yπy/b) sin(n_zπz/c),
  with the corresponding eigenvalues E_nx,ny,nz = [π²ħ²/(2m)][(n_x/a)² + (n_y/b)² + (n_z/c)²].

Problem:

A particle of mass m is in a cubical well of side L, corresponding to the potential energy function
U(r) = 0 if |x|, |y| and |z| < L/2,  U(r) = ∞ otherwise.
(a)  What is its ground-state energy?
(b)  What is the energy of the first excited state?  Is this energy level degenerate or non-degenerate?  Explain!
(c)  Suppose 20 identical, non-interacting particles of mass m and spin ½ are in this well.  What is the ground state energy of this system?  Is this ground state degenerate or non-degenerate?  Explain!

Solution:

• Concepts:
  The energy eigenvalues of the 3D infinite square well.
• Reasoning?
  The energy eigenvalues of the 3D infinite square well are (n_x² + n_y² + n_z²)E₀, with E₀ = π²ħ²/(2mL²).  Many of the energy levels are degenerate.  Only two spin ½ particles can occupy a state with a unique set of spatial quantum numbers n_x, n_y, n_z.
• Details of the calculations:
  (a)  E_{ground state} = 3E₀.  (n_x = n_y = n_z = 1.)
  Considering only spatial degrees of freedom,  E_{ground state} is non-degenerate.
  (b) E_{1st excited state} = 6E₀.  (One of the n_i equals 2, the other two equal 1.)
  Considering only spatial degrees of freedom,  E_{1st excited state} is 3 fold degenerate.
  (c)  We need to occupy the 10 lowest lying states with a unique set of spatial quantum numbers n_x, n_y, n_z.
  Each will be occupied by 2 particles, one spin up and one spin down.
  E_{lowest state} = 3E₀.  (2 particles)
  E_{1st excited state} = 6E₀.  (6 particles)  (One of the n_i equals 2, the other two equal 1.)
  E_{2nd excited state} = 9E₀.  (6 particles)  (One of the n_i equals 1, the other two equal 2.)
  E_{3rd excited state} = 11E₀.  (6 particles)  (One of the n_i equals 3, the other two equal 1.)
  For the 20 fermions E_{ground state} = 2*3E₀ + 6*6E₀ + 6*9E₀ + 6*11E₀ = 162E₀.
  There is only one possible state with this energy, E_{ground state} of the 20 fermions is non-degenerate.

Spherical box

Problem:

(a)  Determine the energy levels and normalized wave functions ψ(r) of a particle with zero angular momentum in a spherical "potential well" U(r) = 0, (r < a), U(r) = ∞, (r > a).
(b)  Determine the average value of r and r² for each of the energy eigenstates with l = 0.

Solution:

• Concepts:
  Three-dimensional "square" potentials
• Reasoning:
  We are asked to determine the energy levels and normalized wave functions ψ(r) of a particle in a three dimensional square potential.
• Details of the calculation:
  (a)  The Hamiltonian is H = -(h²/(2m)(1/r)(∂²/∂r²)r + L²/(2mr²) + U(r).
  The wave function ψ_klm(r,θ,φ) = R_kl(r)Y_lm(θ,φ) = [u_kl(r)/r]Y_lm(θ,φ) is a product of a radial function R_kl(r) and the spherical harmonic Y_lm(θ,φ).
  The differential equation for u_kl(r) is
  [-(ħ²/(2m)(∂²/∂r²) + ħ²l(l+1)/(2mr²) + U(r)]u_kl(r) = E_klu_kl(r).
  For l = 0 we have [-(ħ²/(2m)(∂²/∂r²) + U(r)]u_k0(r) = E_k0u_k0(r).
  With U(r) = 0, (r < a), U(r) = ∞, (r > a) the solutions are
  u_k0(r) = A sinkr, ka = nπ, k = nπ/a.
  We therefore label u_k0(r) with the quantum number n as u_n0(r).
  E_n0 =  n²π²ħ²/(2ma²) are the energy levels when l = 0.
  ∫|ψ_n00(r,θ,φ)|²d³r = 1, A²∫₀^a sin²(nπr/a)dr = 1,  A = (2/a)^½.
  ψ_n00(r,θ,φ) = (1/(2πa)^½)sin(nπr/a)/r.
  (b)  <r> = (2/a)∫₀^a rsin²(nπr/a)dr = a/2.
  <r²> = (2/a)∫₀^a r²sin²(nπr/a)dr = a²/3 - a²/(2n²π²).

Problem:

Assume that the potential energy of the deuteron is given by
U(r) = -U₀, r < r₀; U(r) = 0, r ≥ r₀.
(a)  Show that the ground state of the deuteron possesses zero orbital angular momentum (l = 0).  Since this is true for any central potential, you may not need the detailed nature of the square well potential.
(b)  Assume that l = 0 and estimate the value of U₀ under the additional condition that the value of the binding energy is much smaller than U₀.

Solution:

• Concepts:
  Three-dimensional square potentials
• Reasoning:
  We have to investigate the properties of the ground state in a three dimensional square potential.

• Details of the calculation:
  (a)  The Hamiltonian of the relative motion of the two particles is
  H = p_r²/(2μ) + L²/(2μr²) + U(r).
  H = H₀ + L²/(2μr²),  H₀ = p_r²/(2μ) + U(r).
  Let ψ_l be the lowest energy eigenfunction of H with orbital angular momentum quantum  number l.
  Hψ_l =  [H₀ +  l(l + 1)ħ²/(2μr²)]ψ_l, 
  E_l^min = ∫ψ_l^*[H₀ +  l(l + 1)ħ²/(2μr²)]ψ_l d³r.
  Let ψ_l+1 be the lowest energy eigenfunction of H with orbital angular momentum quantum number l + 1.
  Hψ_l+1 =  [H₀ +  (l + 1)(l + 2)ħ²/(2μr²)]ψ_l+1, 
  E_l+1^min = ∫ψ_l+1^*[H₀ +  (l + 1)(l + 2)ħ²/(2μr²)]ψ_l+1 d³r.
  E_l+1^min = ∫ψ_l+1^*[H₀ +  (l + 1) l ħ²/(2μr²)]ψ_l+1 d³r + ∫ψ_l+1^*[2(l + 1) ħ²/(2μr²)]ψ_l+1 d³r.
  ∫ψ_l^*[H₀ +  l(l + 1)ħ²/(2μr²)]ψ_l d³r ≤ ∫ψ_l+1^*[H₀ + l (l + 1)ħ²/(2μr²)]ψ_l+1 d³r
  since ψ_l is assumed to be the lowest energy eigenfunction of the Hamiltonian 
  H₀ + l(l+1)ħ²/(2μr²).
  [The operator H₀ + l(l+1)ħ²/(2μr²) = p_r²/(2μ) + U'(r) does not operate on the angular coordinates.  We can write its eigenfunctions as [u(r)/r]f(θ,φ), where f(θ,φ) is arbitrary.  The eigenvalues are determined by
  (-ħ²/(2μ))(d²/dr²)u(r) + U'(r)u(r) = Eu(r).  By assumption, the lowest energy eigenfunction u(r) is u_l(r).]
  Therefore   E_l^min ≤ E_l+1^min and the ground state possesses zero orbital angular momentum.
  (b)  The relative motion of the two particles is described in the same way as the motion of a fictitious particle of reduced mass m in a central potential.  Therefore we have
  Φ₁₀₀(r) = R₁₀(r)Y00θ,φ) = [u₁₀(r)/r]Y₀₀(θ,φ).
  [(-ħ²/(2μ))(∂²/∂r²)+ U(r)]u₁₀(r) = E₁₀u₁₀(r)
  The problem is reduced to a one dimensional "square well problem" with E₁₀ = E < 0.
  
  
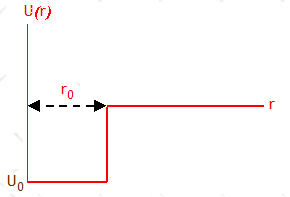
  Define k² = (2μ/ħ²)(E + U₀), ρ² = (2μ/ħ²)(-E), and k₀² = (2μ/ħ²)U₀.
  Let r < r₀ define region 1 and r > r₀ define region 2.  The coordinate r is never negative.  Therefore
  u₁(r) = A sin(kr),  u₁(0) = 0.
  u₂(r) = Bexp(-ρr),  u₂(∞) = 0.
  At r = r₀ we need hat u(r₀) and (∂/∂r)u(r)|_r0 are continuous.
  A sin(kr₀) = Bexp(-ρr₀).
  kA cos(kr₀) = -ρBexp(-ρr₀).
  Therefore cot(kr₀) = -ρ/k.
  1/sin²(kr₀) = 1 + cot²(kr₀) = (k² + ρ²)/k²  = k₀²/k².
  We can find a graphical solution by plotting |sin(kr₀)| and k/k₀ versus k.  The intersections of the two plots in regions where cot(kr₀) < 0 gives the values of k for which a solution exist.
  We need  nπ/2 < kr₀ < (n + 1)π/2, n = odd.
  For only one solution to exist we need the following condition for the slope 1/k₀.
  2r₀/π > 1/k₀ > 2r₀/(3π).
  
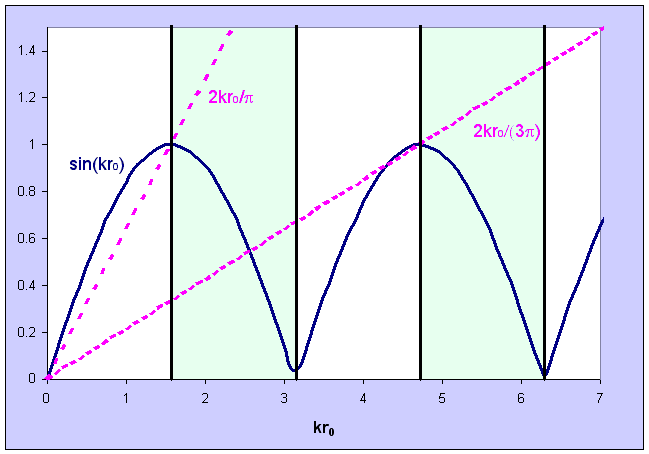
  If |E|<<|U₀|   then  k/k₀ ~ 1.  Then  |sinkr₀| ~ |sink₀r₀| = 1,  k₀r₀ ~ π/2.
  k₀² = (π/2r₀)², U₀ = (π/2r₀)²ħ²/(2μ) ~(π/2r₀)²ħ²/m_p ~ 100 MeV with r₀ = 10^-15 m.

Problem:

Let us represent the interaction between two He atoms by the sum of a short-range repulsive part and a long-range attractive part.
U(r) = + ∞   for r < a,
U(r) = -|U₀|   for a < r < b,
U(r) = 0   for r > b.
(a)  Find the condition satisfied by a, b, and U₀ for a bound state to exist in the relative motion of two He atoms.
(b)  Experimental evidence indicates that He does not solidify at atmospheric pressure, even at ~0 K.  What do you think this implies about the effective helium-helium interaction?

Solution:

• Concepts:
  Three-dimensional square potentials
• Reasoning:
  The radial equation for a particle in a central potential with l = 0 is
  [(-ħ²/(2μ))(∂²/∂r²)+ U(r)]u_k0(r) = E_k0u_k0(r)
  Here U(r) is a square potential, and μ is the reduced mass.
• Details of the calculation:
  (a)  We have to solve a square potential problem in the region 0 < r < ∞.
  Let region 1 extend from r = 0 to r = a, region 2 from r = a to r = b, and region 3 from r = b to infinity.
  In region 1 u = 0.  We need u(a) = u(∞) = 0.
  For bound states we have E < 0. 
  Define k² = (2μ/ħ²)(E + U₀), ρ² = (2μ/ħ²)(-E), and k₀² = (2μ/ħ²)U₀.
  Let us define x = r - a and c = b - a.
  In region 2 we have u₂(x) = A sin(kx), since  u₂(0) = 0.
  In region 3 we have u₃(x) = Bexp(-ρx), since u₂(∞) = 0.
  At x = c we need hat u(c) and (∂/∂x)u(x)|_c are continuous.
  A sin(kc) = Bexp(-ρc)
  kA cos(kc) = -ρBexp(-ρc)
  Therefore cot(kc) = -ρ/k.
  1/sin²(kc) = 1 + cot²(kc) = (k² + ρ²)/k²  = k₀²/k².
  We can find a graphical solution by plotting |sin(kc)| and k/k₀ versus k.  The intersections of the two plots in regions where cot(kc) <  0 gives the values of k for which a solution exist.
  
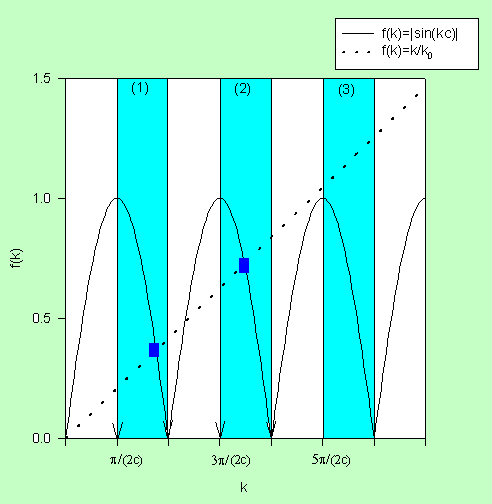
  If the slope 1/k₀ > 2c/π, then no solution exists.
  For a solution to exist we need k₀ > π/(2c), or (2μU₀)^½ > πħ/(2c).
  We need (2μU₀)^½ > πħ/(2b - 2a).
  (b)  Since He does not solidify no bound state exists and we can assume that the condition (2mU₀)^½ > πħ/(2b - 2a) is not satisfied.  The effective helium-helium interaction is either not strong enough or too short range to support a bound state.