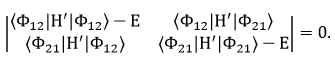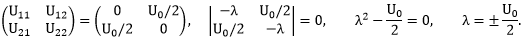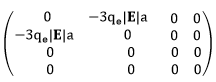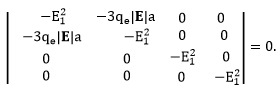Stationary perturbation theory, degenerate states

Problem:

Consider a two-dimensional infinite potential square well of width L,
(U = 0 for 0 < x, y < L, U = infinite everywhere else) with an added perturbation

H' = g sin(2πx/L)sin(2πy/L).

(a)  Calculate the first order perturbation to the ground state energy eigenvalue.
(b)  Calculate the first order perturbation to the first excited state energy eigenvalue.

Solution:

• Concepts:
  Stationary perturbation theory for non-degenerate and for degenerate states
• Reasoning:
  The ground state of two-dimensional infinite potential square well is not degenerate.  The first excited state is two-fold degenerate.
• Details of the calculation:
  H = H₀ + H'.
  The eigenfunctions of H₀ are Φ_nl(x,y) = (2/L)sin(nπx/L)sin(lπy/L), with eigenvalues
  E = (n² + l²)π²ħ²/(2mL²).
  (a)  For the ground state n = l = 1.  The  ground state is not degenerate.
  The unperturbed ground state energy is E₀⁰ = π²ħ²/(mL²).  The first order perturbation correction is
  E₁⁰ = <Φ₁₁|H'|Φ₁₁> = (g4/L²)∫₀^Lsin²(πx/L) sin²(πy/ L)sin(2πx/L) sin(2πy/L)dxdy.
  = (4g/L²)∫₀^Lsin²(πx/L) sin(2πx/L)dx)∫₀^Lsin²(πy/L) sin(2πy/L)dy = 0.

  (b)  The first excited state is two-fold degenerate.
  We can have n = 2, l = 1, or n = 1, l = 2.
  We have to diagonalize the matrix of H' in the subspace spanned by these two degenerate states.
  
  

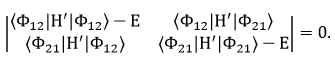
  <Φ₁₂|H'|Φ₁₂> = (4g/L²)∫₀^Lsin²(πx/L)sin(2πx/L)dx)∫₀^Lsin²(2πy/L) sin(2πy/L)dy = 0.
  <Φ₂₁|H'|Φ₂₁> = (4g/L²)∫₀^Lsin²(2πx/L)sin(2πx/L)dx)∫₀^Lsin²(πy/L) sin(2πy/L)dy = 0.
  <Φ₁₂|H'|Φ₂₁> = (4g/L²)∫₀^Lsin(πx/L) sin²(2πx/L)dx)∫₀^Lsin²(2πy/L) sin(πy/L)dy = C
  C = (4g/π²)(∫ ₀^πsin(x) sin²(2x)dx)² = (4g/π²)*64/225.
  <Φ₁₂|H'|Φ₂₁> = (4g/L²)∫₀^Lsin(πx/L) sin²(2πx/L)dx)∫₀^Lsin²(2πy/L) sin(πy/L)dy = C
  E² - C² = 0.  E₁¹ = ±C.  The perturbation removes the degeneracy.

Problem:

A particle of mass m is trapped in a 3-dimensional, infinite square well.
V(x,y,z) = 0, if x, y, and z are less than a and not negative,
V(x,y,z) = ∞, otherwise.
(a)  What are the two lowest energy eigenvalues?  Are these energies degenerate?
(b)  The box is placed into a uniform gravitational field with gravitational acceleration g in the negative z-direction.  Use perturbation theory to calculate first-order corrections to the energy eigenvalues from part (a).

Solution:

• Concepts:
  Three-dimensional square well potentials, perturbation theory
• Reasoning:
  We are supposed to find first order energy corrections to the two lowest energy eigenvalues of the 3D square well.
• Details of the calculation:
  (a)  The eigenfunctions and eigenvalues of the 3D infinite square well are
  Φ_nml(x,y,z) = (2/a)^3/2sin(k_xx)sin(k_yy)sin(k_zz),  with k_x = πn/a,  k_y = πq/a,  k_z = πl/a, n, q, l = 1, 2, ... .
  The associated eigenvalues are
  E_nql = (n² + q² + l²)π²ħ²/(2ma²) = (k_x² + k_y² + k_z²)ħ²/(2m).
  (b)  The two lowest energy eigenvalues are
  E₀¹ = E₁₁₁ = 3π²ħ²/(2ma²),  E₀² = E₁₁₂ = E₁₂₁ = E₂₁₁ = 6π²ħ²/(2ma²). 
  The eigenvalue  E₀² is three-fold degenerate. 
  (b)  The perturbation is W = mgz.
  E₁¹ = <Φ₁₁₁|W|Φ₁₁₁> = (2/a)³mg∫₀^asin²(πx/a)dx ∫₀^asin²(πy/a)dy ∫₀^az sin²(πz/a)dz
  = (2/a)³mg(a/2)⁴ = mga/2 = energy correction for the ground state.
  
  To find the corrections to E₀² and to find out if the degeneracy is removed by the perturbation, we have to diagonalize W in the subspace spanned by Φ₂₁₁, Φ₁₂₁, and Φ₁₁₂.
  <Φ₂₁₁|W|Φ₂₁₁> = (2/a)³mg∫₀^asin²(2πx/a)dx ∫₀^asin²(πy/a)dy ∫₀^az sin²(πz/a)dz = mga/2.
  <Φ₁₂₁|W|Φ₁₂₁> = mga/2.
  <Φ₁₁₂|W|Φ₁₁₂> = (2/a)³mg∫₀^asin²(πx/a)dx ∫₀^asin²(πy/a)dy ∫₀^az sin²(2πz/a)dz = mga/2.
  All the off-diagonal matrix elements of W are zero.  The perturbation does not remove the degeneracy.
  E₁² = mga/2.

Problem:

Consider a charged particle on a ring of unit radius with flux Φ/Φ₀ = a passing through the ring, where Φ₀ = h/(2e) is the flux quantum.  The Hamiltonian operator can be written as H = H₀ + U, where
H₀ = (i∂/∂θ + α)²  and U = U₀ cosθ.
θ is the angular coordinate.  We have chosen units with ħ = 2m = 1.
(a)  Find the complete set of eigenvalues and eigenfunctions of H₀.
(b)  Use perturbation theory to find the first and second-order corrections to the ground state energy E⁰ of H₀ due to the perturbation U for 0 < α < ½ .
(c)  For α = ½ the ground state energy of H₀ is degenerate.  Find the first-order correction to E⁰ for this case.

Solution:

• Concepts:
  First and second order perturbation theory for non-degenerate states, first order perturbation theory for degenerate states.
• Reasoning:
  We find the eigenvalues of H₀, which are non-degenerate if α ≠ ½.  Perturbation theory for nondegenerate states therefore gives the energy corrections.  For α = ½ the ground state is degenerate and perturbation theory for degenerate states must be used.

• Details of the calculation:
  (a)  H₀ψ(θ) = Eψ(θ). 
  Try ψ(θ) = Nexp(ibθ),  H₀exp(ibθ) = (-b + α)²exp(ibθ).
  ψ(θ) = ψ(θ + 2π) -->  exp(ibθ) = exp(ib(θ + 2π)) -->  b = n, n = 0, ±1, ±2, ... .
  ψ(θ) = Nexp(inθ),  Eⁿ = (-n + α)²,
  ∫₀^2π|ψ|²dθ = N²∫₀^2πdθ  = 1 -->  N = (2π)^-½.
  
  (b)  Let 0 < α < ½.  Then all states are non degenerate and the ground state has n = 0. 
  E⁰ = E₀⁰ + E₁⁰ + E₂⁰ + ...,  E₀⁰ = α².  E₁⁰ = <ψ₀|H'|ψ₀> = (2π)^-½U₀∫₀^2πcosθ dθ = 0.
  
  E₂⁰ = ∑_n≠0 |<ψ_n|H'|ψ₀>|²/(E₀⁰ - E₀ⁿ).
  <ψ₀|H'|ψ₀> = (2π)^-1U₀∫₀^2πcosθ exp(inθ)dθ
  = (4π)^-1U₀∫₀^2πexp(i(n+1)θ)dθ + (4π)^-1U₀∫₀^2πexp(i(n-1)θ)dθ
  = δ_n,-1 U₀/2 +  δ_n,+1 U₀/2.
  E₂⁰ = (U₀²/4)/(E₀⁰ - E₀^-1) + (U₀²/4)/(E₀⁰ - E₀¹)
  = -(U₀²/4)[1/(1 + 2α) + 1/(1 - 2)α] = -U₀²/(2 - 8α²)
  
  (c)  If α = ½ then all states are degenerate.  The ground state is any linear combination of n = 0 and n = 1.
  We have to diagonalize the matrix of U in the subspace spanned by
  ψ₀(θ) = (2π)^-½ and ψ₁(θ) = (2π)^-½ exp(iθ).
  
  
  
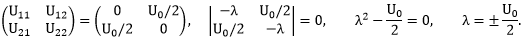
  E₁⁰ = ±U₀/2.
  E₁⁰ = U₀/2, Φ = (1/√2)(ψ₀(θ) + ψ₁(θ)),  E₁⁰ = -U₀/2, Φ = (1/√2)(ψ₀(θ) - ψ₁(θ)).

Problem:

Calculate the splitting induced among the degenerate n = 2 levels of a hydrogenic atom, when this atom is placed in a uniform electric field E pointing in the z-direction.  This is the linear Stark effect.  You may use the following explicit hydrogenic wave functions |nlm>.

|200> = (4π)^-½(2a)^-3/2(2 - r/a)exp(-r/2a),
|211> = (8π)^-½(2a)^-3/2(r/a) exp(-r/2a) sinθ e^iφ,
|210> = (4π)^-½(2a)^-3/2(r/a) exp(-r/2a) cosθ,
|21-1> = (8π)^-½(2a)^-3/2(r/a) exp(-r/2a) sinθ e^-iφ.

∫₀^∞e^-br rⁿ dr = n!/bⁿ⁺¹.
Hint: Exploit symmetries!

Solution:

• Concepts:
  First order perturbation theory, degenerate states
• Reasoning:
  The uniform electric field changes the energy of the proton and the electron and therefore perturbs the Hamiltonian.

• Details of the calculation:
  H = H₀ + q_e|E|z, where z = (z_e - z_p).
  The energy of the proton in the field is -∫₀^zpq_e|E|dz = -q_e|E|z_p.
  The energy of the electron in the field is ∫₀^zeq_e|E|dz = q_e|E|z_e.
  The potential energy of both particles is -q_e|E|(z_p - z_e) = q_e|E|z = -p∙E.
  Let us use first-order perturbation theory.
  The first excited state is 4-fold degenerate.
  E₀² = μe⁴/(8ħ²).
  To find E₁² we have to diagonalize the operator q_e|E|z = q_e|E|r cosθ in the subspace spanned by |200>, |210>, |211>, and |21-1>.  The matrix elements between states with the same parity are zero.  This implies that all diagonal matrix elements are zero and all elements between states with the same l are zero.  The matrix elements between states with different m are zero.  The only matrix elements left are <210|z|200> and <200|z|210>.
  <210|z|200> = q_e|E|(4π)^-1(2a)^-3∫₀^2πdφ∫₀^πcos²θ sinθ dθ ∫₀^∞r³dr (r/a)(2 - r/a) exp(-r/a)
  = -3q_e|E|a.
  We therefore have to diagonalize the matrix
  
  
  
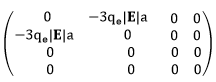
  in the |200>, |210>, |211>, |21-1> basis.
  
  

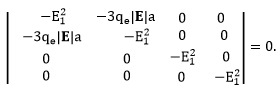
  (E₁²)²[(E₁²)²  - (3q_e|E|a)²] = 0.

  We have (E₁²)² = 0 (two fold degenerate ), or  (E₁²)² = (3q_e|E|a)²_, E₁² = ±(3q_e|E|a)^.
  The eigenvectors corresponding to E₁² = 0 are |211> and |21-1>.
  The eigenvector corresponding to E₁² = 3q_e|E|a is  (1/√2)(|210> - |200>).
  The eigenvector corresponding to E₁² = -3q_e|E|a is (1/√2)(|210> + |200>).
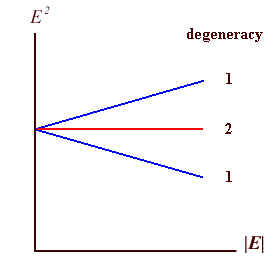
  The four fold degeneracy is changed into two non degenerate eigenvalues and one two fold degenerate eigenvalue.
  

Problem:

Positronium is a bound state of an electron and a positron.
(a)  What is the energy eigenvalue for the 1s state?
(b)  If the spin-spin interaction is neglected, what is the degree of degeneracy of the ground state?
(c)  Assume that the spin-spin interaction is given by AS_e∙S_p, where S_e and S_p are the spin operators for the electron and positron respectively, and A is a coupling constant.  Show that the ground state is split into two states and find the degree of degeneracy of those states.

Solution:

• Concepts:
  Hydrogenic atoms, a system of two spin ½ particles.
• Reasoning:
  Positronium is a hydrogenic atom.  It is a bound state of two spin ½ particles.  The wave function in coordinate space and the energy levels can be obtained from the wave function and energy levels of the hydrogenic atom using scaling rules.
• Details of the calculation:
  (a)  For the hydrogen atom we have E_n = -E_I/n². 
  For a hydrogenic atom we have E_n = -E_I'/n², where E_I' = Z²E_I(μ'/μ).
  In this problem μ' = m_e-m_e+/(m_e- + m_e+) = m_e/2 , Z = 1.
  Therefore E₀ = -13.6/2 eV.
  E₀ is the energy of the 1s (ground) state.
  (b)  The spins of the two particles can combine to form the S = 1 (triplet) and S = 0 (singlet) state.  The ground state is therefore 4-fold degenerate.
  (c)  The energy shift due to the spin-spin interaction is given by
  A <S,M_s|S_e∙S_p|S,M_s>.  S_e∙S_p= ½(S² - S_e² - S_p²).
  S_e∙S_p|S,M_s> = (ħ²/2)(S(S+1) - ½(3/2) - ½(3/2))|S,M_s> = (ħ²/2)(S(S+1) - (3/2))|S,M_s>.
  For the triplet state we therefore have ΔE = ¼ħ²A and for the singlet state we have ΔE = -¾ħ²A.  The singlet state is not degenerate and the triplet state is 3-fold degenerate.

Problem:

A valence electron in an alkali atom is in a p-orbital (l = 1).  Consider the simultaneous interactions of an external magnetic field B = Bk and the spin-orbit interaction.  The two interactions are described by the potential energy
U = (A/ħ²)L·S - (μ_B/ħ)(L + 2S)·B.
(a)  Describe the energy levels of this l = 1 electron for B = 0.
(b)  Describe the energy levels of this l = 1 electron for weak magnetic fields.  Use the projection theorem. (This is the Zeeman effect.)
(c)  Describe the energy levels for strong magnetic fields so that the spin-orbit term in U can be ignored.  (This is called the Paschen-Back effect.)
Projection theorem:  Inside a subspace E(k,j) the matrix elements of the component of a vector observable V are proportional to the matrix elements of the corresponding component of J. 
Therefore <k,j,m_j'|(L+2S)|k,j,m_j> = [<(L+2S)·J>_kj/(j(j + 1)ħ²)] <k,j,m_j'|J|k,j,m_j>.

Solution:

• Concepts:
  Stationary perturbation theory
• Reasoning:
  We use the basis functions {|k,l,s;j,m_j>} and diagonalize U in the subspace defined by a fixed k and l = 1.
• Details of the calculation:
  (a)  B = 0, U = (A/ħ²)L·S.  J = L + S.  L·S = ½(J² - L² - S²).
  L·S is diagonal in the subspace defined by a fixed k and l = 1 and the matrix elements
  <j,m_j|L·S|j,m_j> do not depend on m_j.
  <U>_klj = ½A(j(j + 1) - l(l + 1) - s(s + 1)) = ½A(j(j + 1) - 2 - ¾).   j = ½ or j = 3/2.
  For the p_½ level we have <U> = -A, for the p_3/2 level we have <U> = ½A.
  The p_3/2 level lies 3A/2 above the p_½ level.
  
  (b)  If the magnetic field is weak, we consider U' = - (μ_B/ħ)(L + 2S)·B a perturbation that further splits the p_½ and p_3/2 levels.  For each value of j we diagonalize the perturbation in the subspace spanned by basis functions with different m_j.  We use
  <k,j,m|(L+2S)|k,j,m_j> = [<(L+2S)·J>_kj/(j(j + 1)ħ²)] <k,j,m_j|J|k,j,m_j>. =
  Define g_j =  <(L+2S)·J>_kj/(j(j + 1)ħ²) = Lande g-factor.
  (L+2S)·J = ½(3J² + S² - L²),  <(L+2S)·J>_kj = ½(3j(j + 1) + s(s + 1) - l(l + 1)) ħ².
  g_j = 1 + (j(j + 1) + s(s + 1) - l(l + 1))/(2j(j + 1)).  g_½ = (2/3),  g_3/2 = 4/3 (for l = 1, s = ½).
  <U'>_½ = - (μ_BB/ħ)(2/3)m_jħ = -(2/3)μ_Bm_jB,  <U'>_3/2 =  -(4/3)μ_Bm_jB.
  The weak magnetic field completely removes the degeneracy.
  
  (c)  U = -(μ_B/ħ)(L + 2S)·B = -(μ_BBħ)(L_z + 2S_z)·  (We neglect the spin orbit term.)
  The matrix of U is diagonal in the {|k,l,s;m,m_s>} basis.
  <U>_m,ms = -(μ_BB/ħ)(m + 2m_s)ħ = -μ_BB(m + 2m_s).
  m = -1, 0, 1; 2m_s = -1, 1;
  possible values for m + 2m_s are -2. -1, 0 (two-fold degenerate), 1, 2.
  Each of the levels |k,l,s;m,m_s> can be written as a linear combination of |k,l,s;j,m_j>, and the spin-orbit separates the sublevels with different j.