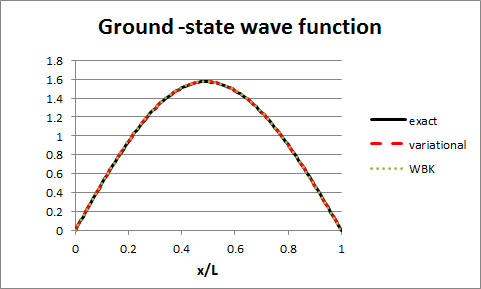
Mixed method problems

Problem:

Consider the 1D infinite well, U(x) = 0 for 0 < x < L, U(x) infinite everywhere else.
The eigenfunctions and eigenvalues of the Hamiltonian for a particle of mass m trapped in this well are
ψ_n(x) = (2/L)^½sin(nπx/L), E_n = n²π²ħ²/(2mL²), respectively.
Now consider the perturbed 1D infinite well, U(x) = 0 for 0 < x < L/2, U(x) = U₀ for L/2 < x < L, U(x) infinite everywhere else.
Let E₀ denote the ground state energy of the unperturbed well.
Assume U₀ = E₀/10 = 0.1*π²ħ²/(2mL²),  i.e. U₀ = 0.1 times the ground state energy of the unperturbed well.

(a)  Solve for the energy eigenvalues of the perturbed well without using an approximation method.
(b)  Solve for the energy eigenvalues of the perturbed well using the WKB approximation.
(c)  Solve for the energy eigenvalues of the perturbed well using 1st order perturbation theory.
(c)  Solve for the lowest energy eigenvalues of the perturbed well using the variational method.

Solution:

• Concepts:
  Comparing approximation methods
• Reasoning:
  We are asked to solve for the energy eigenvalues of the perturbed well using various approximation methods.
• Details of the calculation:
  (a)  No approximation:
  We have a piecewise constant potential.
  Let 0 < x < L/2 define region 1 and L/2 < x < L define region 2.
  The most general solution of the time independent solution in region 1 satisfying the boundary condition at x = 0 is
  ψ₁(x) = A sin(k₁x)
  The most general solution of the time independent solution in region 2 satisfying the boundary condition at x = L is
  ψ₂(x) = B sin(k₂(L-x)).
  Here k₁² = (2m/ħ²)E and k₂² = (2m/ħ²)(E - U₀).
  The boundary conditions are that ψ(x) and (∂/∂x)ψ(x) are continuous at x = L/2.
  A sin(k₁L/2) = B sin(k₂L/2).
  k₁A cos(k₁L/2) = -k₂B cos(k₂L/2).
  This yields tan(k₁L/2)/(k₁L/2) = -tan(k₂L/2)/(k₂L/2).
  This equation can be solved numerically.  We expect solutions for values of k₁L/2 = nπ/2 + ε₁ and k₂L/2 = nπ/2 - ε₂, where ε₁ and ε₂ are small positive numbers.
  Using Excel to find the ground state energy of the perturbed well E₁ we obtain E₁ = 1.04936 E₀. 
  E₁ = E₀ + 0.4936 U₀.
  
  (b)  The WKB approximation:
  In one dimension, if U(x) finite everywhere, then the WKB approximation requires
  ∫_cylcepdx = ∫_cylceħkdx = (n - ½)h n = 1, 2, ... .
  Here U(x) is infinite everywhere except in some finite region and ∫_cylcepdx = ∫_cylceħkdx = nh. 
  ∫₀^L ħkdx = nh/2 = nπħ.  ∫₀^L/2 (2mE)^½dx + ∫_L/2^L (2m(E-U₀))^½dx = nπħ.
  (2mE)^½L/2 + (2m(E - U₀))^½L/2 = nπħ.
  E/4 + (E - U₀)/4 + (E(E - U₀))^½/2 = n²π²ħ²/(2mL²) = n²E₀.
  E/2 - U₀/4 + (E/2)(1 - U₀/E)^½ ~ E/2 - U₀/4 + E/2 - U₀/4 = E - U₀/2 = n²E₀.
  E = n²E₀ + U₀/2, keeping only first order terms in the expansion.
  Higher precision solution of E/2 - U₀/4 + (E/2)(1 - U₀/E)^½ = E₀ we obtain
  E₁ = E₀ + 0.506 U₀.
  
  (c)  First order perturbation theory:
  E_n = n²π²ħ²/(2mL²) + (2/L)∫_L/2^L sin²(πx/l)U₀dx =  n²π²ħ²/(2mL²) + 0.5 U₀.
  E₁ = E₀ +  0.5 U₀.
  
  (d) The variational method:
  We have to choose a trial wave function with an adjustable parameter which satisfies the boundary conditions.
  Choose  ψ(x) = A (2/L)^½(sin(πx/L) + bsin(2πx/L)) = A(ψ₁(x) + bψ₂(x)).
  Normalize: A²(1 + b²) = 1,  A = (1/(1 + b²))^½.
  <H> = <ψ|H|ψ> = -(ħ²/(2m))∫₀^L ψ*(∂²/∂x²)ψ dx + U₀∫_L/2^L ψ*ψ dx.
  <H> = A²E_{1(unperturbed)} + A²b²E_{2(unperturbed)} + U₀[A²∫_L/2^Lψ₁*ψ₁ dx + A²b²∫_L/2^Lψ₂*ψ₂ dx + 2A²b(2/L)∫_L/2^Lsin(πx/L) sin(2πx/L) dx]
  = E₀[(1 + 4b²)/(1 + b²) + 0.1*[0.5(1 + b²)/(1 + b²) - (8/(3π))b/(1 + b²)]
  = E₀[(1 + 4b²)/(1 + b²) + 0.05 - (8/(30π))b/(1 + b²)].
  d<H>/db = 0.  6b - (8/(30π))(1 - b²) = 0.  b² + 22.5π b - 1 = 0.
  b = -11.25 π + ((11.25 π)² + 1)^½ = +0.01414
  <H>_min = E₀*1.0494
  E₁ = E₀ + 0.494 U₀ is the best estimate for the ground state energy using the variational method.
  

Problem:

Let

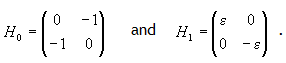
(a)  Find the eigenvalues and eigenvectors of H₀.
(b)  Now derive the expressions for E⁽¹⁾, the change in energy to first order in H₁.  Also derive an equation which must be satisfied for the first order correction |ψ>⁽¹⁾.  Use these results to find E⁽¹⁾ and |ψ>⁽¹⁾ for each of the unperturbed states.
(c)  Now solve (H₀ + H₁)|ψ> = E|ψ> exactly, obtaining both eigenvalues and eigenvectors.  Expand your results to first order in ε and verify that they agree with the results from part (b).  [Note: Your exact answers for the eigenvectors should be normalized.]

Solution:

• Concepts:
  Two-state problem, first-order perturbation theory
• Reasoning:
  We are asked to find the exact eigenvalues of a Hamiltonian operator in a two-dimensional vector space and to find its approximate eigenvalues to first order.
• Details of the calculation:
  (a)  We diagonalize the matrix of H₀.
  
  .
  
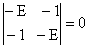  E² = 1, E_± = ±1.  |ψ₊> = 2^-½(|1> - |2>),  |ψ_-> = 2^-½(|1> + |2>).
  
  (b)  For the two state system we have
  H₀|ψ₁⁰> = E₀¹|ψ₁⁰> = 1*|ψ₊>,  H₀|ψ₂⁰> = E₀²|ψ₂⁰> = -1*|ψ_->.
  Let H = H₀ + λW.  Let |ψ₁> and |ψ₂> be the eigenstates of H.
  H|ψ₁> = E¹|ψ₁>,  H|ψ₂> = E²|ψ₂>.
  Assume λW = H₁, and λ is small.
  Since λW is small, we assume that E and |ψ> can be expanded as a power series in λ.
  E^p = E₀^p + λE₁^p + λ²E₂^p + ...  ,
  |ψ_p> = |ψ_p⁰> + λ|ψ_p¹> + λ²|ψ_p²> + ...  . 
  (For the two-state system p can only take on the values 1 or 2.)
  We may then write
  (H₀ + λW)(|ψ_p⁰> + λ|ψ_p¹> + λ²|ψ_p²> + ...)
  = (E₀^p + λE₁^p + λ²E₂^p + ...)(|ψ_p⁰> + λ|ψ_p¹> + λ²|ψ_p²> + ...).
  This equation is must be valid over a continuous range of λ.  Therefore we equate coefficients of equal powers of λ on both sides to obtain a series of equations that represent successively higher orders of the perturbation.
  (i)  (H₀ - E₀^p)|ψ_p⁰> = 0
  (ii)  (H₀ - E₀^p)|ψ_p¹> = (E₁^p - W)|ψ_p⁰>
  (iii)  (H₀ - E₀^p)|ψ_p²> = (E₁^p - W)|ψ_p¹> + E₂^p|ψ_p⁰>
  We choose <ψ_p⁰|ψ_p⁰> = 1.  |ψ_p^s> is not uniquely defined.  We can add an arbitrary multiple of |ψ_p⁰> to each |ψ_p^s> without affecting the left hand side of the above equations.  Most often this multiple is chosen so that <ψ_p⁰|ψ_p^s> = 0.  The perturbed ket is then not normalized.
  Multiplying (ii) by <ψ_p⁰| (and then setting λ = 1) we have  E₁^p = <ψ_p⁰|H₁|ψ_p⁰>.
  E₁^p is the first order energy correction.
  |ψ_p¹> may be written as |ψ_p¹> = ∑_p'b_p'|ψ_p'⁰>.  Here b_p = 0 since <ψ_p⁰|ψ_p¹> = 0.
  For our two-state system we therefore can write
  |ψ₁¹> = b₂|ψ₂⁰>, |ψ₂¹> = b₁|ψ₁⁰>.
  Using (ii) we write
  (H₀ - E₀¹)|ψ₁¹> = (E₁¹ - H₁)|ψ₁⁰>,
  b₂(H₀ - E₀¹)|ψ₂⁰> = b₂(E₀² - E₀¹)|ψ₂⁰> = (E₁¹ - H₁)|ψ₁⁰>.
  Multiplying by <ψ₂⁰| we obtain
  b₂ = <ψ₂⁰|H₁|ψ₁⁰>/(E₀¹ - E₀²).
  Similarly,
  b₁ = <ψ₁⁰|H₁|ψ₂⁰>/(E₀² - E₀¹).
  In this problem
  <ψ₊|H₁|ψ₊> = ½[<1|H₁|1> + <2|H₁|2> - <1|H₁|2> - <2|H₁|1>) = 0.
  <ψ_-|H₁|ψ_-> = ½[<1|H₁|1> + <2|H₁|2> + <1|H₁|2> + <2|H₁|1>) = 0.
  <ψ₊|H₁|ψ_-> = ½[<1|H₁|1> - <2|H₁|2> + <1|H₁|2> - <2|H₁|1>) = ε.
  <ψ_-|H₁|ψ₊> = ½[<1|H₁|1> - <2|H₁|2> - <1|H₁|2> + <2|H₁|1>) = ε.
  Therefore E₁¹ = E₁² = 0, the first order energy corrections are zero.
  E¹ = E₊ and E² = E_- to first order.
  To first order the eigenstates of H are
  |ψ₁> = |ψ₊> + (ε/2)|ψ_->,  |ψ₂> = |ψ_-> - (ε/2)|ψ₊>.
  |ψ₁> = 2^-½[(1 + (ε/2))|1> - (1 - (ε/2))|2>],
  |ψ₂> = 2^-½[(1 - (ε/2))|1> + (1 + (ε/2))|2>].
  
  (c)  We diagonalize the matrix of H.
  
  .
  
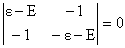  (E - ε)(E + ε) = 1,  E² = 1 + ε²,  E = ±(1 + ε²)^½ ~ ±(1 + ε²/2).
  E¹ = E₊ = 1 and E² = E_- = -1 to first order in ε.
  |ψ₁> = a|1> + b|2>, where a(ε - (1 + ε²)^½) - b = 0,  a² + b² = 1.
  |ψ₂> = c|1> + d|2>, where c(ε + (1 + ε²)^½) - d = 0,  c² + d² = 1.
  Expand and keep only terms up to first order in ε.
  a(ε - 1) - b = 0, a² + a²(ε - 1)² = 1,  a² + a²(1 - 2ε) = 1,
  a² = 1/(2 - 2ε), b² = (1 - 2ε)/(2 - 2ε) ~ (1 - ε)/2
  a ~ 2^-½((1 + (ε/2)),  b ~ -2^-½((1 - (ε/2)).
  c(ε + 1) - d = 0, c² + c²(ε + 1)² = 1,  c² + c²(1 + 2ε) = 1,
  c² = 1/(2 + 2ε), d² = (1 + 2ε)/(2 + 2ε) ~( 1 + ε)/2.
  c ~ 2^-½((1 - (ε/2)),  d ~ 2^-½((1 + (ε/2)).
  If we keep only terms up to first order in ε we get the same solution as in part b.
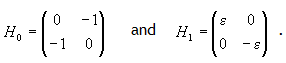
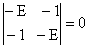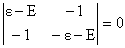