Mixed method problems

Problem:

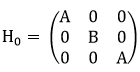
A one-dimensional quantum oscillator consisting of a mass m suspended from a spring with spring constant k is initially in its lowest energy state.  At t = 0, the upper end of the spring is suddenly raised a distance d during a time interval which is very short compared to an oscillator period.
(a)  Give explicit expressions for the time-dependent eigenstates of the Hamiltonian for t < 0 and those for t > 0 and discuss the relationship between them in the context of this problem.
(b) Write down an integral for the probability that a transition has occurred to the first excited state as a result of the disturbance at t = 0.
(c)  Now consider a situation involving the above disturbance at t = 0, followed by an interval from 0 < t < T, where T is large compared with a ground-state period and during which the upper end of the spring remains fixed at the disturbed or stretched position.  At t = T the upper end of the spring is suddenly returned to its lower, original position.
Derive the probability amplitude for the oscillator to be found in its first exited state at times t > T.

The stationary states of H₀ = p²/(2m) + kx²/2 are u_n(x) = N_nH_n(αx)exp(-α²x²/2)
with N_n = [α/(π^½2ⁿn!)]^½, α = (mk/ħ²)^¼  and H_n(αx) a Hermite polynomial.
Recursion relation: H_n+1(αx) = 2αxH_n(αx) - 2nH_n-1(αx).
H₀(αx) = 1,   H₁(αx) = 2αx,   H₂(αx) = 4(αx)² - 2.

Solution:

• Concepts:
  The 1-D harmonic oscillator, the sudden approximation, time-dependent perturbation theory
• Reasoning:
  The system is a 1-D harmonic oscillator.  When the system is suddenly displaced, the sudden approximation can be used to calculate transition probabilities to the eigenstates of the new Hamiltonian.  For a small perturbation that last a finite time, time-dependent perturbation theory can be use to calculate transition probabilities to different eigenstates of H₀.
• Details of the calculation:
  (a)  For t < 0 we have H₀ = p²/(2m) + kx²/2 = (ħ²/2m)∂²/∂x² + kx²/2.
  The eigenfunctions of H₀ are u_n(x,t) = u_n(x)exp(-iE_nt/ħ), with
  E_n = (n + ½)ħω, ω = (k/m)^½.
  The u_n(x) are given, u_n(x) = N_nH_n(ax)exp(-a²x²/2).
  For t > 0 the system is displaced by a distance Δx = d.
  H = (ħ²/2m)∂²/∂x² + k(x-d)²/2.
  Let x' = x-d.  Then (ħ²/2m)∂²/∂x'² + kx'²/2.
  The eigenfunctions are u_n'(x,t) = u_n(x')exp(-iE_nt/ħ) = u_n(x-d)exp(-iE_nt/ħ).
  
  (b)  Here we calculate the probability of finding the system in the first excited state of the perturbed Hamiltonian H.  This probability does not change with time.  We use the sudden approximation.
  P₀₁ = |<u₀(x)|u₁(x-d)>|² = N₀²N₁²|∫_-∞^∞dx 2α(x-d)exp(-α²x²/2)exp(-α²(x-d)²/2)|².
   = [α²/(2π)]|∫_-∞^∞dx 2α(x-d)exp(-α²x²/2)exp(-α²(x-d)²/2)|².
  (c)  A perturbation is turned on at t = 0 and turned off at t = T.  Here we calculate the probability of finding the system in the first excited state of the unperturbed Hamiltonian H₀ at time T.  This probability changes with T.
  H = H₀ + H',  H' = -kdx + ½kd².
  Time-dependent perturbation theory yields
  P₀₁(t > T) = (1/ħ²)|∫₀^Texp(iω₁₀t')H'₁₀dt'|²,  ω₁₀ = (E₁ - E₀)/ħ = ω = (k/m)^½.
  H'₁₀ = -kd<u₁|x|u₀>.
  <u₁(x)|x|u₀(x)> = N₀N₁∫_-∞^∞dx H₁(αx) x H₀(αx) exp(-α²x²)
  = N₀N₁(½α)∫_-∞^∞dx  (H₂(αx) + 2H₀(αx)) H₀(αx) exp(-α²x²)
  = N₀N₁(1/α)∫_-∞^∞dx H₀²(αx) exp(-α²x²) = N₁/(N₀α).
  P₀₁(t > T) = (N₁²/(N₀²α²ħ²)|∫₀^Texp(iωt')dt'|² 
  = (N₁²/(N₀²α²ħ²)(4/ω²)sin²(ωT/2) = 2/(α²ħ²ω²)sin²(ωT/2).

Problem:

(a)  An electron is located in the ground state in a 1D potential well,
U(x) = 0, 0 < x < L, U(x) = ∞ elsewhere. 
Instantaneously the well becomes 1.5 times wider.  What is the probability for the electron to go directly to ground state in this new well?

(b)  An electron is located in the ground state in a 1D potential well,
U(x) = 0, 0 < x < L, U(x) = ∞ elsewhere.   
For a time interval ∆t, the well bottom is disturbed, and the potential energy function becomes U(x) = 0, 0 < x < L/2, U(x) = U₀, L/2 < x < L, with U₀ << than the ground state energy.  After the time interval ∆t the disturbance is removed.  What is the probability for the electron to be in the first excited state of the well at a time t = 2∆t? 

Solution:

• Concepts:
  The sudden approximation, time dependent perturbation theory
• Reasoning:
  We are asked to recognize when these approximation methods can be used.
• Details of the calculation:
  For a particle in an infinite well we have
  ψ_n(x,t) = (2/L)^½sin(nπx/L)exp(-iE_nt/ħ).  E_n = n²π²ħ²/(2mL²).
  (a)  Sudden approximation:
  The probability that the electron to goes directly into the ground state of the new well is
  P = |<ψ₁(1.5L)|ψ₁(L)>|² = [(2/L)^½(4/3L)^½ ∫₀^L dx sin(πx/L) sin(2πx/3L)]².
  ∫₀^L dx sin(πx/L) sin(2πx/3L) = (3L/π)∫₀^π/3 dy sin(3y) sin(2y)
  = (3L/π)[sin(y)/2 - sin(5y)/10]| ₀^π/3 = (3L/π)(3√3)/10.
  P = (8/3)(9/π²)(27/100) = 0.66.

  (b)  Time dependent perturbation theory
  During the time the perturbation is applied, the probability P(E₂,t) of finding the system in the eigenstate |2> of H₀ at time t, i.e . the probability of measuring the eigenvalue E₂, is given by
  P(E₂,t) = (1/ħ²)|∫₀^texp((i/ħ)(E₂-E₁)t')<Φ₂|W|Φ₁>dt'|²
  = |(<Φ₂|W|Φ₁>/ħ)∫₀^texp(iω₂₁t')dt'|².
  [∫₀^texp(iω₂₁t')dt' = (-i/ω₂₁)(exp(iω₂₁t) - 1)
  = (-i/ω₂₁)exp(iω₂₁t/2)(exp(iω₂₁t/2) - exp(-iω₂₁t/2))
  = (2/ω₂₁)exp(iω₂₁t/2)sin(ω₂₁t/2)]
  P(E₂,t) = (|<Φ₂|W|Φ₂>|²/(ħω₂₁)²) 4 sin²(ω₂₁t/2).
  ω₂₁ = 3π²ħ/(2mL²).
  <Φ₂|W|Φ₁> = (2/L)U₀ ∫_L/2^L dx sin(2πx/L) sin(πx/L) = -4U₀/(3π).
  P(E₂,t) = (16/9)²(m²L⁴U₀²/(ħ⁴π⁶))sin²(3π²ħt/(4mL²)).
  P(E₂,∆t) = (16/9)²(m²L⁴U₀²/(ħ⁴π⁶))sin²(3π²ħ∆t/(4mL²)).
  For t > ∆t, Φ₂ is an eigenstate of the Hamiltonian and the probability for the electron to be in the first excited state does not change.
  P(E₂,2∆t) = (16/9)²(m²L⁴U₀²/(ħ⁴π⁶))sin²(3π²ħ∆t/(4mL²)).

Problem:

Consider a system of two non-identical spin ½ particles.  For t < 0 the particles do not interact and the Hamiltonian may be taken to be zero.  For t > 0 the Hamiltonian is given by

H = (4Δ/ħ²) S₁∙S₂,

where Δ is a constant.  For t < 0 the state of the system is |+ ->. 
(a)  For t > 0, find, as a function of time, the probability for finding the system in each of the states |+ +>, |+ ->, |- +>, and |- ->, by solving the problem exactly.
(b)  For t > 0, find, as a function of time, the probability for finding the system in each of the states |+ +>, |+ ->, |- +>, and |- ->, using first-order time dependent perturbation theory with H a perturbation that is switched on at t = 0.
(c)  Under what condition is the perturbation calculation a bad approximation to the exact solution, and why?

Solution:

• Concepts:
  The state space of two spin ½ particles, time-dependent perturbation theory.
• Reasoning:
  S₁∙S₂ = ½(S² - S₁² - S₂²).  The eigenstates of S₁∙S₂ are the singlet state and the triplet states,
  {|S, M_s>}, S = 0, 1.
  |1,1> = |+ +>
  |1,0> = ½^½(|+ -> + |- +>),  |1,-1> = |- ->,  |0,0> = ½^½(|+ -> - |- +>)
  Therefore |+ -> = ½^½(|0,0> + |1,0>), |- +> = ½^½(|0,0> - |1,0>).
• Details of the calculation:
  (a)  For the singlet state we have S₁∙S₂|0, 0> = -¾ħ²,   H|0, 0> = -3∆| 0, 0>.
  For the triplet states we have S₁∙S₂|1, M_s> = ¼ħ²,   H |1, M_s> = ∆|1, M_s>.
  
  |ψ(t)> = U(t, 0)|+ -> = 2^-½(exp(i3∆*t/ ħ)|0,0> + (exp(-i∆*t/ ħ)|1,0>)
  P(t) of being in the state |+ +> = |1, 1> = 0.
  P(t) of being in the state |- -> = |1, -1> = 0.
  
  P(t) of being in the state |+ -> = |<+ -| ψ(t)>|².
  <+ -| ψ(t)> =  ½(exp(i3∆*t/ ħ) + (exp(-i∆*t/ ħ))
  = ½ exp(i∆*t/ ħ) (exp(i2∆*t/ ħ) + (exp(-i2∆*t/ ħ)) = exp(i∆*t/ ħ) cos(2∆*t/ ħ).
  P(t) of being in the state |+ -> = cos²(2∆*t/ ħ).
  For 2∆*t/ ħ << 1, P(t) ~ 1.
  
  P(t) of being in the state |+ -> = sin²(2∆*t/ ħ), since the total probability of being in one of the 4 basis states must be equal to 1.
  For 2∆*t/ ω_fi << 1, P(t) ~ (2∆*t/ ħ)².

  (b)  Time-dependent perturbation theory
  P_if(t) = (1/ħ²)|∫₀^texp(iω_fit')W_fi(t')dt'|².
  The initial and the final state must be different for this formula to be valid.  For i = f, P(t) ~ 1.

  W_fi = <f|H|i>.  Here W_fi = <f|H |+ ->. 
  W_fi = 0 for |f> = |+ +> an |f> = |- ->, so P_if(t) = 0 for these states.

  For |f> = |- +> W_fi = 2^-½<- +|H| (|00> + |10>)
  = 2^-½[-3∆<- +| 0, 0> + ∆<- +| 1, 0>] = ½ (-3∆ - ∆) = -2∆.

  ω_fi = (E_f - E_i)/ω_fi = 0 for the unperturbed states.

  P_if(t) = (1/ħ²)|∫₀^t(-2∆)dt'|² = 4∆²t²/ ħ².

  (c)  The time-dependent perturbation theory calculation result agrees with the exact result as long as x = 2∆*t/ ħ << 1, so that cos(x) = 1 and sin(x) = x are very good approximations.  For large x (or t) the probability of finding the particle in the state |- +> oscillates between 0 and 1.

Problem:

Consider a 3-state system with a Hamiltonian

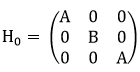
in the {|i>} orthonormal basis, i = 1, 2, 3, with B, A > 0.  For < 0, the system is in state |1>.
At t = 0 the Hamiltonian suddenly changes to

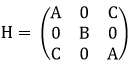
with C << A, B, C > 0.
At t = T the Hamiltonian changes back to H₀.
(a)  What are the eigenstates and eigenvalues if H expressed in terms of the {|i>} basis vectors?
(b)  For each of the eigenstates of H, what are the probabilities that the system will be found in this state for 0 < t < T?
(c)  Using first order time-dependent perturbation theory, what is the probability of finding the system in state |3> at t' > T?
(d)  Solve part (c) exactly.

Solution:

• Concepts:
  Transition probabilities, the sudden approximation, time-dependent perturbation theory, the exact solution
• Reasoning:
  We are asked to find transition probabilities,
• Details of the calculation:
  (a) The eigenvalues of H are E₁ = A + C,  E₂ = B,  and E₃ = A - C.
  The corresponding eigenvectors are |1'> = 2^-½(|1> + |3>),   |2'> = |2>,  |3'> = 2^-½ (|1> - |3>}.
  (b)  For 0 < t < T the probabilities of finding the system in states |1'> and |3'> are ½, the probability of finding the system in state |2'> is zero.
  (c)  For a constant perturbation
  P₁₃(t) = (|<3|W|1>|²/(ħω₃₁)²)4 sin²(ω₃₁t/2).
  Since ω₃₁ = 0,  we have P₁₃(t) = |<3|W|1>|²t²/ħ² = C² t²/ħ².
  The perturbation is turned off at t = T,  so for t' > T we have P₁₃(t') = C² T²/ħ².
  (d)  |1> = 2^-½(|1'> + |3'>).
  For 0 < t < T  |Ψ(t)> = 2^-½(|1'> exp(-i(A + C)t/ ħ) + |3'> exp(-i(A - C)t/ ħ)).
  For  t' > T  |Ψ(t')> = 2^-½(|1'> exp(-i(A + C)T/ ħ) + |3'> exp(-i(A - C)T/ ħ)) exp(-i(A(t' - T)/ ħ),
  since |Ψ(t')>  is an eigenstate of H₀.
  |Ψ(t')> = 2^-½(|1'> exp(-iCT/ ħ) + |3'> exp(iCT/ ħ)) exp(-i(A(t'/ ħ)
  = ½[|1>(exp(-iCT/ ħ) + exp(iCT/ ħ)) + |3>(exp(-iCT/ ħ) - exp(iCT/ ħ))] exp(-i(A(t'/ ħ).
  <3||Ψ(t')> = i sin(CT/ ħ) exp(-i(A(t'/ ħ).
  P₁₃(t') = |<3||Ψ(t')>|² = sin²(CT/ ħ).
  If CT/ ħ  << π/2 then P₁₃(t') = C² T²/ħ².  Then first order perturbation theory is a valid approach.

.