Other scattering problems

Problem:

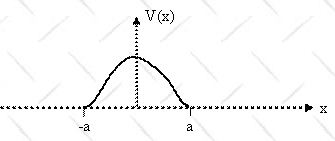
V(x) is an arbitrary repulsive potential localized at a position along the x-axis as shown below.

The solution of the Schroedinger equation must be of the form
ψ(x) = A e^ikx + B e^-ikx  for x < -a,
ψ(x) = C e^ikx + D e^-ikx  for x > a.
Write

,

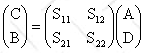and assume A and B are arbitrary complex numbers.  Use conservation of flux to show that
|S₁₁|² + |S₂₁|² = |S₁₂|² + |S₂₂|² = 1,
and that
S₁₁S₁₂^* + S₂₁S₂₂^* = 0.
Show that S is a unitary matrix.

Solution:

• Concepts:
  Probability flux
• Reasoning:
  Flux conservation requires that the flux into a region is equal to the flux out of that region.
• Details of the calculation:
  Flux: j(x,t) =[ħ/(2mi)][ψ*(x,t) ∂ψ(x,t) ∂x - ψ*(x,t) ∂ψ(x,t) ∂x]
  Here j(x,t) = [ħk/m][|A|² - |B|²] for x < -a and j(x,t) = [ħk/m][|C|² - |D|²] for x > a.

  Flux conservation requires that |A|² - |B|² = |C|² - |D|², or |A|² + |D|² = |C|² + |B|².
  (Flow into the region where V(x) is not zero equals flow out of the region where V(x) is not zero.)
  C = S₁₁A + S₁₂ D.  B = S₂₁A + S₂₂D.
  |C|² + |B|² = |S₁₁|²|A|² + |S₁₂|²|D|² + S₁₁S₁₂^*AD^* + S₁₁^*S₁₂A^*D + |S₂₁|²|A|² + |S₂₂|²|D|² + S₂₁S₂₂^*AD^* + S₂₁^*S₂₂A^*D
  = (|S₁₁|² + |S₂₁|²)|A|² + (|S₁₂|² + |S₂₂|²)|D|² + (S₁₁S₁₂^* + S₂₁S₂₂^*)AD^* + (S₁₁^*S₁₂ +S₂₁^*S₂₂)A^*D
  = |A|² + |D|².
  This implies that
  |S₁₁|² + |S₂₁|² = 1, |S₂₂|² + |S₁₂|² = 1,  S₁₁S₁₂^* + S₂₁S₂₂^* = 0.

  .

  Similarly 
  , 
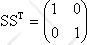  S is unitary.