

Let Es(1) denote the two-dimensional state space of particle 1 and Es(2) the two-dimensional state space of particle 2. Es= Es(1)ÄEs(2) then is the state space of the system of the two particles. Es is four-dimensional.
The vectors {|i:+>,|i:->} form a basis for the two-dimensional state space of each particle. They are eigenvectors of Siz and Si2. Here i denotes either particle 1 or particle 2.
![]() ,
,
![]() .
.
The vectors {|++>,|+->,|-+>,|-->}, (where |++>=|1:+>Ä|2:+> etc. ), form a basis for Es. Every vector in Es can be written as a linear combination of these basis vectors.
Let e denote + or -. The we express orthogonality through
![]() ,
,
and completeness through
![]() .
.
The most general normalized state in Es is
![]() ,
,
with ![]() .
.
In the four dimensional state space of the two particles Siz and Si2 are product operators.
![]() etc.
etc.
The matrix of any product operator A(1)ÄB(2) in a basis of tensor product vectors {|i(1)>Ä|j(2)>=|i,j>} is
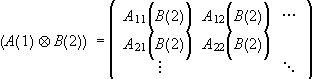 ,
,
where the Aij are the matrix elements of A in the {|i(1)>}
basis of E1 and ![]() is the
matrix of B in the {|j(2)>} basis of E2.
is the
matrix of B in the {|j(2)>} basis of E2.
![]()
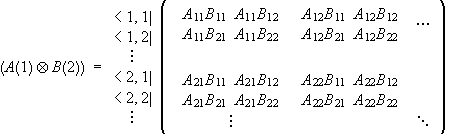 .
.
The matrix of S1z in the {|++>,|+->,|-+>,|-->} basis therefore is
 .
.
The matrix of S2z is
 .
.
The matrix of S12 and S22 is
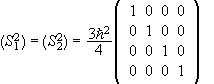 .
.
What do we see inspecting these matrices?
The basis vectors {|++>,|+->,|-+>,|-->} are eigenvectors of S1z, S2z, S12, and S22 in Es.
The total spin of the two particles is S=S1+S2. What are the eigenvectors of S2 and Sz?
![]() .
.
Any linear combination of basis vectors are eigenvectors of S12 and S22. To find the eigenvectors of S2 we therefore have to find the eigenvectors of S1·S2.
![]() .
.
In the {|++>,|+->,|-+>,|-->} basis we have
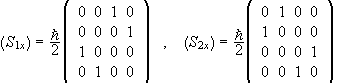 .
.
 .
.
 .
.
What do we see by inspecting these matrices?
The basis vectors are not eigenvectors of Six, Siy,
![]() , and S2.
, and S2.
The eigenvalues of S2 are 0 and ![]() . The eigenvalue
. The eigenvalue ![]() is 3 fold degenerate.
is 3 fold degenerate.
Any linear combination of the normalized vectors |++>, ![]() is an eigenvector with eigenvalue
is an eigenvector with eigenvalue ![]() .
.
The eigenvector with eigenvalue 0 is ![]() .
.
The matrix of Sz=S1z+S2z is
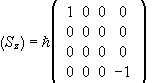
in the {|++>,|+->,|-+>,|-->} basis.
Common eigenvectors of S2 and Sz are |++>, ![]() and
and ![]() .
Each common eigenvector is uniquely
specified by its pair of eigenvalues. These eigenvectors also form a basis of Es,
which we denote by {|S,Sz>}, where
.
Each common eigenvector is uniquely
specified by its pair of eigenvalues. These eigenvectors also form a basis of Es,
which we denote by {|S,Sz>}, where ![]() denotes the eigenvalue of S2
and
denotes the eigenvalue of S2
and ![]() denotes the eigenvalue of Sz.
We have
denotes the eigenvalue of Sz.
We have
![]() ,
,
triplet states
and
![]() .
.
singlet state
S2 and Sz form a C.S.C.O. for the 4-dimensional state space Es.
(a) Write the Hamiltonian for the system.
(b) Work out the matrix form of H, defining the basis states explicitly.
(c) Find the exact expressions for the energies of the eigenstates.
(d) Calculate the state energies using perturbation theory and compare these approximate results with your exact expressions from part c).
![]()
![]() .
.
Let us choose the {|++>,|+->,|-+>,|-->} basis. Then

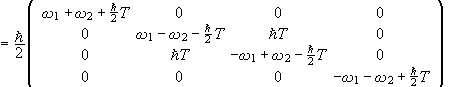 .
.
(c) ![]() .
The l are the eigenvalues of H.
We have (since the matrix
is block-diagonal)
.
The l are the eigenvalues of H.
We have (since the matrix
is block-diagonal)
![]() ´
´
![]() =0,
=0,
where ![]() .
One of the factors in this product has to be zero.
.
One of the factors in this product has to be zero.
The eigenvalues are
![]() ,
,
and from ![]()
![]()
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
A system of two distinguishable spin ½ particles (S1 and S2) are in some triplet state of the total spin, with energy E0. Find the energies of the states, as a function of l and d, into which the triplet state is split when the following perturbation is added to the Hamiltonian, V=l(S1xS2x+S1yS2y)+dS1zS2z.
In the { |S,Sz> }={|1,1>,|1,0>,|1,-1>,|0,0>} basis the matrix of the Hamiltonian H0 is
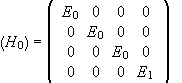 .
.
We have H=H0+V.
![]() .
.
In the { |S,Sz> } the matrix of V is diagonal, since the
matrices of ![]() are diagonal.
are diagonal.
![]() .
.
For the triplet state ![]() .
.
For the singlet state ![]() .
.
![]() ,
,
![]() .
.
Therefore we have
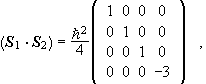
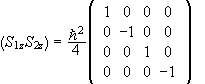 .
.
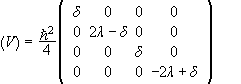 ,
,
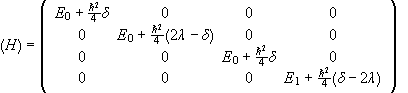 .
.
The energies into which the triplet state splits are ![]() and
and ![]() . The value
. The value ![]() is twofold
degenerate.
is twofold
degenerate.