

Assume that at t=-„ a system is in an eigenstate |fi> of the Hamiltonian H0. At t=t1 the system is perturbed and the Hamiltonian becomes H=H0+W(t). When investigating the interaction picture we found that the probability of finding the system in the eigenstate |ff> of the Hamiltonian H0 at t=t2 is given by
![]()
to first order in the perturbation W.
We often write
![]()
![]()
This is the result of first order time dependent perturbation theory.
![]()
![]()
![]()
![]()
![]()
For the harmonic perturbation W(t)=Wsinwt, we find that
![]()
has an appreciable amplitude only if the denominator of one of the two terms is approximately zero, i.e. if
![]() The first order effect of a
perturbation that varies sinusoidally with time is to receive from or transfer to the
system a quantum of energy
The first order effect of a
perturbation that varies sinusoidally with time is to receive from or transfer to the
system a quantum of energy ![]()
If the system is initially in the ground state, then Ef>Ei, and only the second term needs to be considered. Then
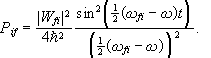
Let b=wfi-w,
and plot 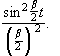

If b=0, i.e. wfi=w, then 
Therefore, if wfi=w,
then the probability of finding the system in the state |ff>,
![]() increases linearly with time.
increases linearly with time.
In the above figure the height of 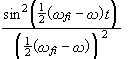 increases
proportional to t2, and the width of the peak is proportional to 1/t.
The area under the curve is proportional to t.
increases
proportional to t2, and the width of the peak is proportional to 1/t.
The area under the curve is proportional to t.
For a first order approximation to be valid, we need ![]()
On the other hand, to justify neglecting the first term in the above formula, we need 2wfi>>Dw. 2wfi is the difference in the positions of the peaks due to the first term and the second term in the above formula, Dw is the width of the peaks, Dw»4p/t. We therefore need
![]()
Combining these two conditions we obtain
![]()
![]()
Assume there is a group of states n, nearly equal in energy E, and that Wni=<fn|W|fi> is
nearly independent of n for these states. Take for example continuum
states.
We may
label continuum states by |a>, where a is continuous. <a|a>=d(a-a').
The probability of making a transition to one of these states
in a small range Da is ![]() If |a>=|b,E> then da=r(b,E)dE,
where r(b,E) is
the density of states. We assume b
to be some discrete index. We then have
If |a>=|b,E> then da=r(b,E)dE,
where r(b,E) is
the density of states. We assume b
to be some discrete index. We then have
![]()
If W is a constant perturbation, then
![]()

The function 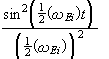 peaks at wEi=0 and has an appreciable amplitude only in a small
interval DwEi or DE
about wEi=0. We assume that r(b,E) and |WEi|2
are nearly constant in that small interval and therefore may be taken out of the integral.
Then
peaks at wEi=0 and has an appreciable amplitude only in a small
interval DwEi or DE
about wEi=0. We assume that r(b,E) and |WEi|2
are nearly constant in that small interval and therefore may be taken out of the integral.
Then
![]()
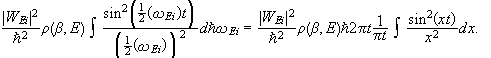
![]()
Therefore,
![]()
It is understood that the expression is integrated with respect to dE.
The transition probability per unit time is the given by Fermi’s golden rule,
![]()
Similarly, for a sinusoidal perturbation W(t)=Wsinwt or W(t)=Wcoswt we obtain
![]()
and for W(t)=Wexp(±iwt) we obtain
![]()
Let ![]()
We have ![]() (Coulomb or radiation
gauge)
(Coulomb or radiation
gauge)
![]()
![]()
We have a plane electromagnetic wave propagating in the y-direction.
Let ![]() and
and ![]() with E0
and B0 real,
with E0
and B0 real, ![]() ( SI
units ) Then
( SI
units ) Then
![]()
S is the Poynting vector.
The Hamiltonian of an atomic electron interacting with this plane wave is
![]()
In this expression we consider only one independent electron, and we neglect the spin orbit interaction. We have
![]()
[pz,Az]=0 since Az depends only on y.
![]()
![]()
To find induced transition probabilities, we have to evaluate the matrix elements of W(t) between unperturbed bound states. An order of magnitude estimate reveals
![]()
in the optical domain. We assume that the intensity of the wave is low enough so that WIII, the term containing A02, can be neglected compared to terms containing A0.
![]()
![]() since y is on the order of
atomic dimensions.
since y is on the order of
atomic dimensions.
Let WDE(t) be the zeroth order term in the expansion.
![]()
WDE is called the electric dipole Hamiltonian. The electric dipole approximation assumes W(t)=WDE(t).
Note: This form of WDE is equivalent to the form we would get starting with the energy of an electric dipole in an electric field.
![]()
This equivalence can be shown via a gauge transformation ![]()
![]()
![]()
![]()
The matrix elements of WDE are proportional to the matrix elements of z, because E is in the z direction.
![]()
![]()
The integrant is a product of three spherical harmonics and the integral can be given in terms of Clebsch Gordan coefficients.
![]()
![]()
These are coefficients ![]()
The integral is zero unless
since ![]()
![]() We therefore have that
We therefore have that ![]() unless
unless ![]() If we
choose another direction for the polarization of E, i.e.
If we
choose another direction for the polarization of E, i.e. ![]() then we find
then we find ![]()
The dipole transition selection rules therefore are
![]()
These selection rules result as a consequence of the properties of the spherical harmonics.
An electromagnetic field is most likely to induce a transition between an initial and a final state if these selection rules are satisfied. If these selection rules are not satisfied a transition is less likely and is said to be forbidden.
When deriving the dipole transition selection rules Dl=±1,
Dm=0, ±1, we assumed that the Hamiltonian ![]() was perturbed by WDE(t).
We neglected the spin orbit interaction. If H0 contains a spin orbit
coupling term f(r)L·S, then the eigenstates of H0
are
was perturbed by WDE(t).
We neglected the spin orbit interaction. If H0 contains a spin orbit
coupling term f(r)L·S, then the eigenstates of H0
are
{|l,s;j,mj>} and not {|l,s;m,ms>}. The dipole selection rules then become Dj=0, ±1, (except ji=jf=0), Dl=±1, Dmj=0, ±1.
(p or r are vector operators. The selection rules follow from the Wigner-Eckart theorem.)
![]()
![]()
if we take the first order term in the expansion of exp(±iky). We may write ![]()
If in the expression for WII(t) we only keep the zeroth order term in
the expansion of exp(±iky), ![]() then
we are looking at terms of similar magnitude. We write
then
we are looking at terms of similar magnitude. We write
![]() called the magnetic
dipole Hamiltonian, and
called the magnetic
dipole Hamiltonian, and
![]() called the electric
quadrupole Hamiltonian.
called the electric
quadrupole Hamiltonian.
Transition induced by WDM obey the magnetic dipole transition selection rules
![]()
or, if H0 includes a spin orbit coupling term,
![]()
Transition induced by WQM obey the electric quadrupole transition selection rules
![]()