

The eigenvalue equation for the Hamiltonian H0 of a particle with potential energy -Ze2/r is
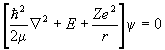 .
.
Common eigenfunctions of H0, L2, and Lz are of the form ynlm(r)=Rnl(r)Ylm(q,f).
![]() .
.
If E>0, then a solution exists for any value of E and l.
If E<0, then solutions exist only for discrete values of E, ![]() .
.
| n=1 | ground state | ionization potential | |
| n=2 | resonance level | resonance potential |
For hydrogen EI=13.595eV, ER=10.196eV.
| K | L | M | N | O |
| 1s | 2s | 3s | 4s | 5s |
| 2p | 3p | 4p | 5p | |
| 3d | 4d | 5d | ||
| 4f | 5f | |||
| 5g |
The probability per unit time of a spontaneous transition
from a stationary state |a> to a stationary state |b>, accompanied by
the emission of a photon of energy ![]() =Ea-Eb
is
=Ea-Eb
is
![]() ,
,
with xab=<a|x|b>.
The selection rules are Dl=±1, Dml=0, ±1, Dn is not restricted.
![]() .
.
R=109677.581cm-1 for hydrogen.
| n'=1 | n=2,3,4,… | Lyman series |
| n'=2 | n=3,4,5,… | Balmer series |
| n'=3 | n=4,5,6,… | Paschen series |
| n'=4 | n=5,6,7,… | Bracket series |
| n'=5 | n=6,7,8,… | Pfund series |
I=neutral, II=singly ionized, III=doubly ionized, … .
(Example: BeI, BeII, BeIII, … .)
H=H0+Hf.
![]() .
.
First order energy shifts:
![]() .
.
Dipole selection rules: Dj=0, ± 1, Dmj=0, ± 1.
The Hamiltonian H0 for a multi-electron atom is
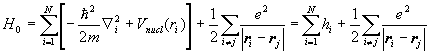 .
.
H0y=Ey.
We often use the central field approximation. We assume that each electron moves in a centrally symmetric field created by the nucleus and all the other electrons. Let U(ri) denote the potential energy of electron i in the centrally symmetric field of all the other electrons.
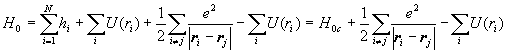 .
.
H=H0c+H'. We treat the non-central part of the potential as a perturbation of H0c. This perturbation is referred to as electron-electron correlations.
To solve H0cy=Ey for the eigenfunctions and eigenvalues of H0c, we assume that y is of the form y=y1(r1)y2(r2)… . Then the eigenvalue equation can be separated into equations of the form
 .
.
For each electron we therefore have an equation of the form
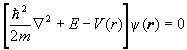 .
.
The solutions are of the form y(r)=R(r)Ylm(q,f)c(x), where R(r) is a solution to the radial equation
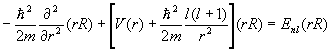 .
.
We have N independent equations. The central field approximation is therefore called an independent electron approximation.
To calculate U(ri) due to the centrally symmetric field produced by all the other electrons, we must know the wave functions of all electrons.
Procedure:
The wave function y thus found is the optimum wavefunction that can result from a variational calculation with a trial function of the form y=y1(r1)y2(r2)….
In the central field approximation 2(2l1+1)2(2l2+1)2(2l3+1) states, differing by the values of the quantum numbers ml and ms correspond to each configuration n1l1, n2l2, n3l3,… . The non-central part of the electrostatic interaction between the electrons and the spin-orbit interaction lead to splitting of the level n1l1, n2l2, n3l3,… into a number of sublevels.
We assume that the non-central part of the electrostatic interaction is much bigger than the spin-orbit interaction. (This is usually true for light multi-electron atoms.) The electrostatic interaction leads to a splitting of the level corresponding to a given electron configuration into a number of sublevels characterized by different values of the total orbital angular momentum of the electrons, L, and the total spin, S. The operator for the electrostatic interaction commutes with L=l1+l2+l2+… and S=s1+s2+s3+… . (See Cohen-Tannoudji, page1000). To each term LS belong (2L+1)(2S+1) states, differing by the values of ML and MS. The spin-orbit interaction leads to a splitting of the term LS into a number of components corresponding to different values of the total angular momentum J. But it does not completely remove the degeneracy. Each J component is degenerate with a multiplicity of 2J+1.
![]() .
.
In the LS coupling scheme, a term is designated by 2S+1LJ. 2S+1 is called the multiplicity of the term.
Which terms corresponding to a given configuration have the lowest energy?
Hund's Rule (established empirically)
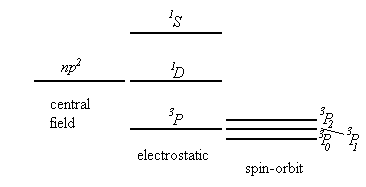
| np, n'p | [1S] | n''p | ----> | 2P |
| np, n'p | [1P] | n''p | ----> | 2S, 2P, 2D |
| np, n'p | [1D] | n''p | ----> | 2P, 2D, 2F |
| np, n'p | [3S] | n''p | ----> | 2P, 4P |
| np, n'p | [3P] | n''p | ----> | 2S, 2P, 2D, 4S, 4P, 4D |
| np, n'p | [3D] | n''p | ----> | 2P, 2D, 2F, 4P, 4D, 4F |
In brief form this is written as
| 2S P D F | 4S P D F |
| 2 6 4 2 | 1 3 2 1 |
The number under the term symbol indicates the number of identical terms.
Among the values of L and S obtained from the general rules for addition of angular momenta are those which correspond to states forbidden by the Pauli principle.
For each electron the following values are
possible:
ml=1,0,-1, ms=1/2,-1/2
Combining the different values of ml and ms, we
obtain the following possible states:
| ml=1 | ms=1/2 | (1+) |
| ml=0 | ms=1/2 | (0+) |
| ml=-1 | ms=1/2 | (-1+) |
| ml=1 | ms=-1/2 | (1-) |
| ml=0 | ms=-1/2 | (0-) |
| ml=-1 | ms=-1/2 | (-1-) |
In each of these states there cannot be more than one electron.
The following states with non-negative values of ML and Ms are possible.
| State | ML | Ms |
| (1+)(0+) | 1 | 1 |
| (1+)(-1+) | 0 | 1 |
| (1+)(1-) | 2 | 0 |
| (1+)(0-) | 1 | 0 |
| (1+)(-1-) | 0 | 0 |
| (0+)(1-) | 1 | 0 |
| (0+)(0-) | 0 | 0 |
| (-1+)(1-) | 0 | 0 |
State with negative values of ML and Ms need not be written out.
Thus only three terms are possible, 1D, 3P, and 1S for the configuration np2.
The statistical weight is the total number of terms pertaining to a given configuration.
For a configuration with no equivalent electrons the statistical weight is
![]() .
.
For the configuration ln, the statistical weight is determined by the number of possible combinations which can be formed from the quantum numbers ml, ms taking into account the Pauli principle. Let N0=2(2l+1). The statistical weight of ln is
![]() .
.
We assume that the spin-orbit interaction considerably exceeds the non-central part of the electrostatic interaction. (This is usually true for heavy multi-electron atoms.) Then the energy depends primarily on how the orbital angular momentum li and the spin angular momentum si of each electron sum up into the total angular momentum ji of each electron. j1=l1+s1, j2=l2+s2, … . The electrostatic interaction now leads to a splitting, depending on how the vectors ji sum up into the total angular momentum J. In the jj coupling scheme the state of each electron is described by four quantum numbers, n, l, j, mj, where j=l ±1/2.
1s1/2, 2s1/2, 2p1/2, 2p3/2, …
If we neglect the electrostatic energy completely, then the energy of each electron is determined by the quantum numbers nlj. The level corresponding to each j is 2j+1 fold degenerate.
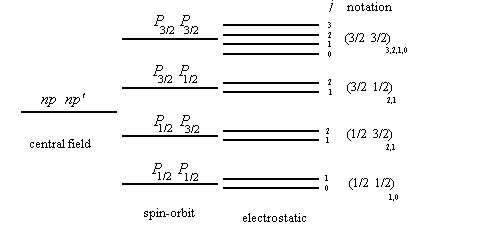
| possible terms | ||
| np1/2 , np1/2 | m1=1/2, m2=-1/2 | (1/2,1/2)0 |
| np1/2 , np3/2 | m1= ±1/2, m2= ±1/2, ±3/2 | (1/2,3/2)2,1 |
| np3/2 , np3/2 | m1=3/2, m2=1/2 m1=3/2, m2=-1/2 m1=3/2, m2=-3/2 m1=1/2, m2=-1/2 |
(3/2,3/2)2,0 |