

In this lab students will build two laser-beam expanders.
The output of a laser is different than that of most other light sources. The laser resonator determines the spatial characteristics of the laser beam. Most lasers have spherical-mirror Fabry-Perot resonators that have Hermite-Gaussian spatial modes. Usually only the lowest order transverse resonator (TEM00) mode oscillates, resulting in a Gaussian output beam.
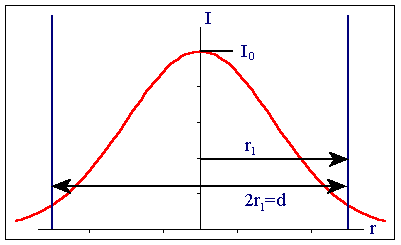
For a Gaussian beam the irradiance of the beam is symmetric about the beam axis and varies with radial distance r from the axis as
I(r) = I0exp(-2r2/r12)
Here r1 is the radial extent of the beam where the irradiance has dropped to 1/e2 of its value on the beam axis, I0.
![]()
A Gaussian beam has a waist, where r1 is smallest. It either diverges from or converges to this beam waist. This divergence or convergence is measured by the angle θ which is subtended by the points on either side of the beam axis where the irradiance has dropped if to 1/e2 of its value on the beam axis.
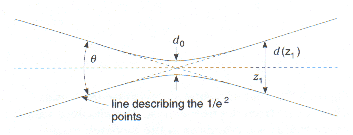
Under the laws of geometrical optics a Gaussian beam converging at an angle of θ should collapse to a point. Because of diffraction, this does not occur. However, at the intersection of the asymptotes that define θ, the beam diameter reaches a minimum value d0, the beam waist diameter. For a TEM00 mode d0 depends on the beam divergence angle as d0 = 4λ/πθ, where λ is the wavelength of the radiation.
For a Gaussian beam of a particular wavelength, the product d0θ is constant. Therefore, for a beam with a very small beam waist d0 the divergence θ must be large, while for a highly collimated beam with small θ the beam waist d0 must be large.
The variation of the beam diameter in the vicinity of the beam waist is given by
d2 = d02 + θ2z2,
where d is the diameter at a distance ąz from the waist along the beam axis.
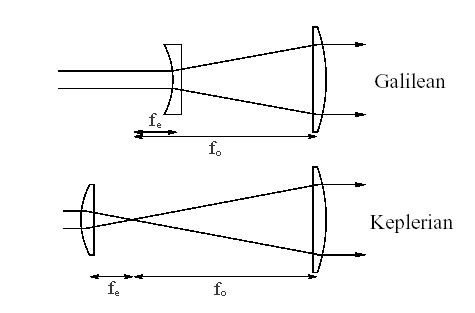
Some applications require a laser beam with low divergence. To reduce θ we must expand the waist of the beam. This can be achieved by expanding a laser beam with a beam expander. A beam expander consists of two lenses. First, the beam is diverged with a short focal length lens and then the diverging beam is re-collimated with a larger beam waist and smaller divergence. The lenses are positioned like in an inverted telescope. The light enters in the eyepiece lens and emerges from the objective lens.
We have
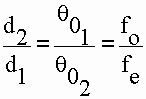
After passage through a beam expander, the divergence of the beam is equal to its original divergence divided by the power of the telescope fo/fe.
In this experiment students will construct two types of laser beam expanders, a Galilean and a Keplerian beam expander.
![]()
|
Laser Assembly | |
|
Beam Steering Assemblies | |
|
Lens Chuck Assemblies | |
|
Target Assembly | |
|
Lens Kit | |
|
Meter Stick | |
|
Index Cards | |
|
Project in Optics Workbook |
![]()
Students will generally follow the instructions on pages 56 - 58 of the Projects in Optics Workbook. Exceptions are noted below. To assemble the components, students will refer to pages 36 - 44 in the Projects in Optics Workbook.
|
In step 1 in the workbook, mount the laser assembly so so that the rod and the rod clamp are flush on top. This assures that you have enough freedom of movement for the lenses. |

|
In step 2 in the workbook, first make sure that the laser beam reflects back onto itself before rotating the mirror. Use lens paper in the beam path to observe the incident as well as the reflected beam and adjust the mirror so that the reflected beam overlaps the incident beam. | |||||||||
|
In step 3 in the workbook, first adjust the second beam steering assembly so that the laser beam reflects back onto itself, then rotate the mirror so that the beam strikes the target. | |||||||||
In step 4 you are supposed to find the initial divergence of the laser beam. This may be difficult given space restrictions. Try it by determining the beam diameter at 5 distances from the laser aperture. Record your measurements in a table. After you have completed your data analysis, compare your results with the specifications of the manufacturer. For the He-Ne lasers used in the Optics Laboratory you can assume that the beam waist is located at the output aperture of the laser. Note that d0θ = 4λ/π.
| |||||||||
|
In step 5, first rotate the mirror of the second beam steering assembly back, so that the laser beam reflects back onto itself before inserting the lens into the beam path. Place lens paper at various positions between the lens and the mirrors. Observe the primary beam and the reflected beam on the lens paper. This can make alignment easier. | |||||||||
|
In step 6, use the lens paper as in step 5. |

![]()
Construct an Excel spreadsheet with at least 5 rows of data points:
| original beam |
expanded beam 1 Galilean expander |
expanded beam 2 Keplerian expander |
|||||||||||
| z | d | z2 | d2 | z | d | z2 | d2 | z | d | z2 | d2 | ||
Plot d2 versus z2 for the original beam and the expanded beams. Use Excel's Data Analysis regression function to find the slope of the best fitting straight line and the error in that slope. From this determine θ and Δθ, the uncertainty in θ.
![]()
Open Microsoft Word and prepare a report using the template shown below.
| In a few words, describe the experiment. (What?) | |
| In a few words, state the objective of the experiment. (Why?) | |
| Comment on the procedure. Did you encounter difficulties or surprises? (How?) | |
| Present your results and comment on your results. |