

In this lab students will build a Twyman-Green interferometer and use it to determine the frequency separation of the axial modes of a He-Ne laser.
![]()
A LASER (Light Amplification by Stimulated Emission of Radiation) is an electromagnetic oscillator which combines light amplification with feedback. The laser uses mirrors to feed the light output from an optical amplifier through a delay (the travel time of the light) back into the amplifier input.
Atoms and molecules can interact with light by three related processes, absorption, spontaneous emission, and stimulated emission. Stimulated emission is the process which provides optical amplification in most lasers. An excited atom or molecule can be stimulated to release its excess energy E in response to an incident photon of the right frequency (f = E/h ). The atom emits an additional photon with the same frequency f, resulting in an amplification factor of exactly two.
An optical resonator constructed with two mirrors that face each other provides feedback and delay.
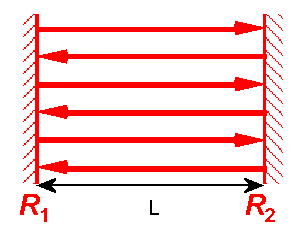
The mirrors re-circulate, or feed back, the light with efficiency R = R1R2, the product of the reflectivities of the two mirrors. The delay time τ = 2L/c is the time it takes light to complete a round trip between the mirrors. The net gain for a complete round must be equal to unity to sustain steady oscillation, the gain must exactly compensate for the loss.
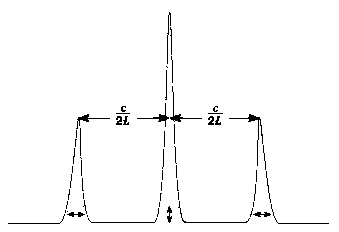
There is an additional criterion that after each round trip the light wave crests line up with the crests from the previous round trip. This results in a standing wave. The condition on the mirror separation is that one round trip contains an integral number of wavelengths 2L = mλ, where m is an integer. The corresponding resonant frequencies are fm = c/λ = mc/(2L). The separation between resonance frequencies is Δf = c/2L.
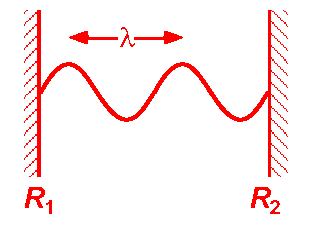
A typical visible wavelength laser resonator might have length L = 30 cm operating at wavelength λ = 600 nm so that m = 1 million. For an L = 30 cm resonator, the spacing between successive resonance frequencies is Δf = c/2L = 500 MHz while the resonance frequencies are near fm = c/λ = 500 THz, one million times larger.
![]()
The frequency of the laser transition can lie in a range Δf about f = E/h, since the energy of the levels has an uncertainty ΔE. Several of the resonance frequencies fm may fall into that range Δf. The spectrum emitted by a laser is a combination of the resonant frequencies fm that fall into that range Δf. A representative laser output spectrum is shown below.
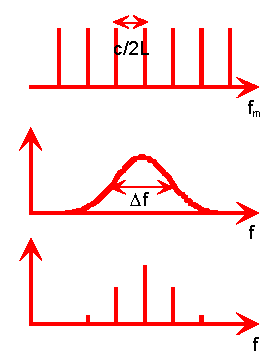
Modified laser resonators can suppress all but one of the resonant frequencies, permitting more precise control of the frequency, a desirable feature in scientific and engineering applications.
![]()
The He-Ne laser in the "Projects in Optics" kit supports three axial modes. The polarization of neighboring modes is orthogonal. It is possible to investigate these modes without resorting to high-resolution devices by using the Twyman-Green interferometer.
Assume our source emits waves with wavelength λ1 and λ2. Waves with wavelength λ1 and λ2 emitted in phase, will destructively interfere after some optical path length l'c = λ2/(2Δλ); l'c is often also called the coherence length. This definition of the coherence length differs from our previous definition by a factor of π.
[The phase of a wave propagating into
the x-direction is given by φ = kx - ωt. Look at the wave pattern in space at
some time t. After some distance l the phase difference
between two waves with wave vectors k1 and k2 which are
in phase at x = 0 becomes Δφ = (k1 - k2)l.
When Δφ = π,
the two waves interfere destructively.
We therefore have
π = (k1 - k2)l'c
= (2π/λ - 2π/(λ + Δλ))l'c.
(λ + Δλ - λ)l'c/(λ(λ + Δλ)) ~ Δλl'c/λ2
= 1/2.
l'c
= λ2/(2Δλ).]
Since λf = c, we have Δf/f
= Δλ/λ.
We can write
l'c
= λ2/(2Δλ)
= λf/(2Δf)
= c/2Δf,
If we can measure l'c, we can calculate Δf = c/2l'c.
Using the interferometer, we can measure the coherence length by monitoring the contrast of the fringes. When the interference maxima and minima of neighboring modes with λ1 and λ2 overlap, we observe high contrast fringes. If we move one of the mirrors a distance ΔL = l'c/2, so that the total path increases by l'c, then the maxima of one mode will overlap the minima of the neighboring mode and the fringe contrast will be greatly reduced. We have
Δf = c/2l'c = c/(4ΔL).
![]()
|
Laser Assembly | |
|
Beam Steering Assemblies | |
|
Lens Chuck Assemblies | |
|
Target Assemblies | |
|
Lens Kit | |
|
Beam Splitter | |
|
Optical Rail | |
|
Meter Stick | |
|
Index Cards | |
|
Project in Optics Workbook |
![]()
Follow the instructions on pages 71 - 74 of the Projects in Optics Workbook. To assemble the components, refer to pages 36 - 44 in the Projects in Optics Workbook.
Required:
|
Complete steps 1 - 10 as described in the workbook. Mount the laser, the first mirror, and the beam expander directly onto the breadboard. Mount the second mirror, the beam splitter, and the reference mirror onto the optical rail. You should be able to move the reference mirror at least 30 cm back from the position it has when it has the same distance from the beam splitter as the test mirror. | |||||||||||||||
|
Start your experiment with the reference mirror and the test mirror having approximately the same distance from the beam splitter. Carefully move the reference mirror about its initial position to find the mirror position that gives the strongest possible fringe contrast. Record the reference mirrors distance from the beam splitter in a table.
| |||||||||||||||
|
Complete 11 - 14 as described in the workbook. Try to find positions of minimum, maximum, and minimum fringe contrast. Record these positions in the table. | |||||||||||||||
|
Complete steps 15 and 16 as described in the workbook. Calculate Δf from your measurements. Estimate Δf based on the exterior dimensions of the laser. Does your measurement seem reasonable? |
Optional:
|
Add a polarizer to the system and carry out the additional experiments as described on page 74 of the workbook. |
![]()
Open Microsoft Word and prepare a report using the template shown below.
| In a few words, describe the experiment. (What?) | |
| In a few words, state the objective of the experiment. (Why?) | |
| Comment on the procedure. Did you encounter difficulties or surprises? (How?) | |
| Present your results and comment on your results. |