

Assume we want light to get from point A to point B, subject to some boundary condition. For example, we want the light to bounce off a mirror or to pass through a piece of glass on its way from A to B. Fermat's principle states that of all the possible paths the light might take, that satisfy those boundary conditions, light takes the path which requires the shortest time.
(A more accurate statement of Fermatís principle: Any hypothetical small change in the actual path of a light ray would only result in a second order change in the optical path length. The first order change in the optical path length would be zero.)
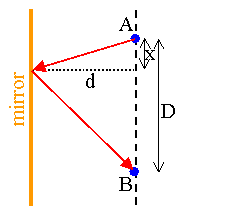
| Consider the diagram on the right. We want light to leave point A, bounce off the mirror, and
get to point B. Let the perpendicular distance from the mirror of both A and B be d and
the shortest distance between the points be D. Assume that light takes the path shown.
The
length of this path is
L = (x2 + d2)1/2 + ((D - x)2 + d2)1/2. Since the speed of light is the same everywhere along all possible paths, the shortest path requires the shortest time. To find the shortest path, we differentiate L with respect to x and set the result equal to zero. (This yields an extremum in the function L(x).)
After canceling equal terms on both sides we are left with d2D2 = 2Dx, or x = D/2. The path that takes the shortest time is the one for which x = D/2, or equivalently, the one for which θi = θr. Fermat's principle yields the law of reflection. |
 |
| Now assume we want light to propagate from point A to point B across the boundary
between medium 1 and medium 2. For the path shown in the figure on the right the time required is
Setting dt/dx = 0 we obtain
or n1sinθ1 = n2sinθ2. Fermat's principle yields Snell's law.
|
 |
In Fermat's Principle the optical path length between points A and B can be calculated in either direction, A to B or B to A, the result is the same. This leads to the principle of geometrical reversibility.
Principle of Ray Reversibility: Any actual ray of light in an optical system, if reversed in direction, will retrace the same path backward.