Electromagnetic waves

Electromagnetic (EM) waves are changing electric and magnetic fields, transporting energy and momentum through space. EM waves are solutions of Maxwell's equations, which are the fundamental equations of electrodynamics. EM waves require no medium, they can travel through empty space. Sinusoidal plane waves are one type of electromagnetic waves. Not all EM waves are sinusoidal plane waves, but all electromagnetic waves can be viewed as a linear superposition of sinusoidal plane waves traveling in arbitrary directions. A plane EM wave traveling in the x-direction is of the form

E(x,t) = E_maxcos(kx - ωt + φ), B(x,t) = B_maxcos(kx - ωt + φ).

E is the electric field vector, and B is the magnetic field vector of the EM wave. For electromagnetic waves E and B are always perpendicular to each other and perpendicular to the direction of propagation. The direction of propagation is the direction of E x B.

If, for a wave traveling in the x-direction E = Ej, then B = Bk and j x k = i. Electromagnetic waves are transverse waves.

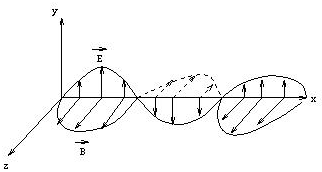The wave number is k = 2π/λ, where λ is the wavelength of the wave. The frequency f of the wave is f = ω/2π, ω is the angular frequency. The speed of any periodic wave is the product of its wavelength and frequency.

v = λf.

The speed of any electromagnetic waves in free space is the speed of light c = 3*10⁸ m/s. Electromagnetic waves can have any wavelength λ or frequency f as long as λf = c.

When electromagnetic waves travel through a medium, the speed of the waves in the medium is v = c/n(λ_free), where n(λ_free) is the index of refraction of the medium. The index of refraction n is a properties of the medium, and it depends on the wavelength λ_free of the EM wave. If the medium absorbs some of the energy transported by the wave, then n(λ_free) is a complex number. For air n is nearly equal to 1 for all wavelengths. When an EM wave travels from one medium with index of refraction n₁ into another medium with a different index of refraction n₂, then its frequency remains the same, but its speed and wavelength change. For air n is nearly equal to 1.

The electromagnetic spectrum

Electromagnetic waves are categorized according to their frequency f or, equivalently, according to their wavelength λ = c/f. Visible light has a wavelength range from ~400 nm to ~700 nm. Violet light has a wavelength of ~400 nm, and a frequency of ~7.5*10¹⁴ Hz. Red light has a wavelength of ~700 nm, and a frequency of ~4.3*10¹⁴ Hz.

Visible light makes up just a small part of the full electromagnetic spectrum. Electromagnetic waves with shorter wavelengths and higher frequencies include ultraviolet light, X-rays, and gamma rays. Electromagnetic waves with longer wavelengths and lower frequencies include infrared light, microwaves, and radio and television waves.

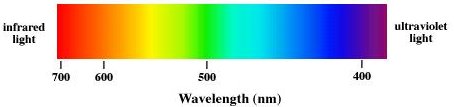Polarization

Polarization is a phenomenon peculiar to transverse waves. Longitudinal waves such as sound cannot be polarized. Light and other electromagnetic waves are transverse waves made up of mutually perpendicular, fluctuating electric and magnetic fields. In the diagram on the right an EM wave is propagating in the x-direction, the electric field oscillates in the xy-plane, and the magnetic field oscillates in the xz-plane. A line traces out the electric field vector as the wave propagates.

For a linearly polarized electromagnetic wave traveling in the x-direction, the angle the electric field makes with the y-axis is unique.

An unpolarized electromagnetic wave traveling in the x-direction is a superposition of many waves. For each of these waves the electric field vector is perpendicular to the x-axis, but the angle it makes with the y-axis is different for different waves. For unpolarized light traveling in the x-direction E_y and E_z are randomly varying on a timescale that is much shorter than that needed for observation.

The diagram on the light depicts unpolarized light. Natural light is, in general, unpolarized.

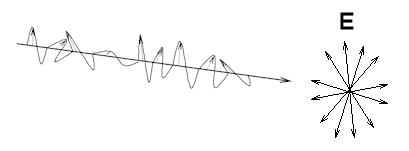Electromagnetic waves transport energy through space. In free space this energy is transported by the wave with speed c. The magnitude of the energy flux S is the amount of energy that crosses a unit area perpendicular to the direction of propagation of the wave per unit time. It is given by

S = EB/(μ₀) = E²/(μ₀c),

since for electromagnetic waves B = E/c. The units of S are J/(m²s). μ₀is a constant called the permeability of free space, μ₀ = 4π*10^-7 N/A².

Note:
The energy transported by an electromagnetic wave is proportional to the square of the amplitude, E², of the wave.

The Poynting vector is the energy flux vector. It is named after John Henry Poynting. Its direction is the direction of propagation of the wave, i.e. the direction in which the energy is transported.

S = (1/μ₀)E x B.

Energy per unit area per unit time is power per unit area. S represents the power per unit area in an electromagnetic wave. If an electromagnetic wave falls onto an area A where it is absorbed, then the power delivered to that area is P = S∙A.

The time average of the magnitude of the Poynting vector, <S>, is called the irradiance or intensity. The irradiance is the average energy per unit area per unit time. <S> = <E²>/(μ₀c) = E_max²/(2μ₀c).

EM wave also transport momentum. The momentum flux is S/c. The magnitude of the momentum flux S/c is the amount of momentum that crosses a unit area perpendicular to the direction of propagation of the wave per unit time. If an electromagnetic wave falls onto an area A where it is absorbed, the momentum delivered to that area in a direction perpendicular to the area per unit time is dp_perp/dt = (1/c)S∙A.

The momentum of the object absorbing the radiation therefore changes. The rate of change is dp_perp/dt = (1/c)SA_perp, where A_perp is the cross-sectional area of the object perpendicular to the direction of propagation of the electromagnetic wave. The momentum of an object changes if a force is acting on it.

F_perp= dp_perp/dt = (1/c)SA_perp

is the force exerted by the radiation on the object that is absorbing the radiation. Dividing both sides of this equation by A_perp, we find the radiation pressure (force per unit area) P = (1/c)S. If the radiation is reflected instead of absorbed, then its momentum changes direction. The radiation pressure on an object that reflects the radiation is therefore twice the radiation pressure on an object that absorbs the radiation.

Photons

Electromagnetic waves transport energy and momentum across space. The energy and momentum transported by an electromagnetic wave are not continuously distributed over the wave front. Energy and momentum are transported by photons in discrete packages. Photons are the particles of light. Light is "quantized". Photons always move with the speed of light. The energy of each photon is E = hf = hc/λ. The momentum of each photon is E/c = hf/c = h/λ.

(h = 6.626*10^-34J s = 4.136*10^-15 eV s
unit of energy: 1 eV = 1.6*10^-19 J
useful product: hc = 1240 eV nm)

So what is an electromagnetic wave, a wave or a stream of photons? What is our current understanding of the nature of light and other EM waves?

Quantum mechanics views photons as quanta or packets of energy. But these quanta behave nothing like macroscopic particles. For a macroscopic particle we assume that we can measure its position and its velocity at any time with arbitrary precision and accuracy. Given that we have done this, we can predict with arbitrary precision and accuracy its subsequent motion. But for any photon, we can only predict the probability that the photon will be found at a given position. That probability can be calculated using the wave equation for electromagnetic waves. Where the wave equation predicts a high light intensity, the probability is large, and where it predicts a low light intensity, the probability is small.