

We can classify optical phenomena into one of three categories: ray optics, wave optics, and quantum optics.
In many situations, the wavelengths of the light being studied are very small compared to the dimensions of the equipment used to study the light, and the photon energies are much smaller than the energy sensitivity of the equipment. Under these conditions we can make an approximation called geometrical optics or ray optics.
Consider the wavelength scale of light waves. Wavelengths in the middle of the visible band are on the order of 500 nm. So a laser beam with a diameter of 1 mm has a diameter of 2000 wavelengths. Individual atoms in a solid are separated by distance on the order of 0.1 nm. So, as far as visible light is concerned, matter is quasi-continuous.
If the wavelengths of the light become comparable to the dimensions of the equipment, but the photon energies are still negligibly small, then we study optical phenomena using the classical theory of radiation, or wave optics. Wave optics contains all of ray optics, but the mathematical treatment is much more involved. When the photon energies become comparable to the sensitivity of the equipment, we must study the phenomena using quantum optics.
![]()
| We define a ray as the path along which light energy is transmitted
from one point to another in an optical system. The basic laws of
geometrical optics are the law of reflection and the law of refraction. If
not being reflected or refracted, a light ray travels in a straight line.
The optical path length of a ray traveling from point A to point B is defined as
c times the time it takes the ray to travel from A to B. Assume a ray travels a distance d1 in a medium with index of refraction n1 and a distance d2 in a medium with index of refraction n2. The speed of light in a medium with index of refraction n is c/n. The travel time from A to B therefore is t = n1d1/c + n2d2/c. The optical path length is OPL = n1d1 + n2d2. |
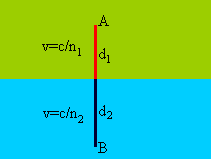 |
The index of refraction for various media:
| absolute vacuum | n = 1 | v = c |
| air | n = 1.0003 | v = 0.9997 c |
| water | n = 1.33 | v = 0.75 c |
| glass | 1.4 < n < 1.8 | 0.56 c < v < 0.71 c |
| diamond | n = 2.4 | v = 0.42 c |
| silicon | n = 3.5 | v = 0.29 c |
![]()
The subject of geometrical optics starts with the laws of refraction and reflection for transparent media. These laws are used to discover the properties of various optical systems, which may contain any number of curved refracting and reflecting surfaces. In principle one could solve any optical problem by the exact application of the basic laws. However, it is possible to derive some very useful general results by using approximate forms of the laws, which treat only rays, called paraxial rays, which make small angles with respect to an optical axis. Often the treatment is confined to spherical surfaces. This approximate form of the basic laws as applied to paraxial rays in an optical system consisting of spherical surfaces is called the first order theory and constitutes a major part of the subject of geometrical optics.