

Conjugate Planes
Let Pí be the image of a point P formed by some system of lenses. P and Pí are called conjugate points and they lie in conjugate planes.
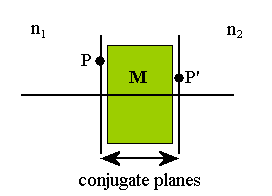
The geometry and refracting characteristics of the optical system are contained in the transformation matrix M. If r1 characterizes a ray entering the optical system at P and r2 characterizes that same ray exiting the system at Pí, then
 .
.
Since Pí is an image of P, x2 must be independent of θ1. We need M21 = 0.
We then have x2 = M22x1. Since x2/x1 is the lateral magnification mx, we have mx = M22.
For θ2 we have
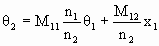 .
.
For two different rays leaving x1 and arriving at x2 we therefore have
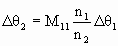 .
.
If we define the ray angle magnification mθ = Δθ2/Δθ1, then we have
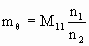 .
.
Since the determinant M equals 1, M11*M22 = 1.
This yields mxmθ(n2/n1) = 1, or (x2/x1)(Δθ2/Δθ1)(n2/n1) = 1, or n1x1Δθ1 = n2x2Δθ2 .
This is called the Lagrange equation, nxΔθ is known as the Lagrange invariant.
In terms of mx and mθ the overall transformation matrix between conjugate planes may be written as
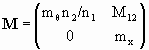 .
.