

Details:
Medium 1 and medium 2 are two homogeneous media with a common interface. The index of refraction of medium 1 is n1 and the index of refraction of medium 2 is n2. A ray, incident in medium 1, strikes the interface at a point P. Let n be the unit vector normal to the interface at P, pointing from medium 1 to medium 2. Let s denote the unit vector pointing in the direction of propagation of the ray in medium 1, and let s make an angle θ1 with n. Let t be a unit vector tangential to the interface in the plane containing both s and n.
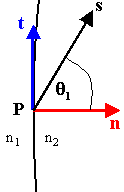
In terms of its components along the perpendicular directions defined by n and t we may write
s = cosθ1n + sinθ1t
or
n1s = n1cosθ1n + n1sinθ1t.
(equation 1)
At the interface the ray may be refracted or reflected. Let us first consider the refracted ray. Let s denote the unit vector pointing in the direction of propagation of the refracted ray; s make an angle θ2 with n.
In terms of its components along the perpendicular directions defined by n and t we may write
s = cosθ2n + sinθ2t
or
n2s = n2cosθ2n + n2sinθ2t.
The law of refractions states that n1sinθ1 = n2sinθ2.
Therefore
n2s = n2cosθ2n + n1sinθ1t.
(equation 2)
Combining equations 1 and 2 yields
n2s = n1s + (n2cosθ2 - n1cosθ1)n.
(equation 3)
![]()
A ray at a spherical interface
Now let us consider a spherical interface. Let the radius of curvature be |R|, and let the center of curvature C lie on the z-axis of our coordinate system. Let the vertex V be the point where the surface intersects the z-axis. Let us consider R to be positive if the z-coordinate of C is greater than the z-coordinate of V and negative if the z-coordinate of C is less than the z-coordinate of V.
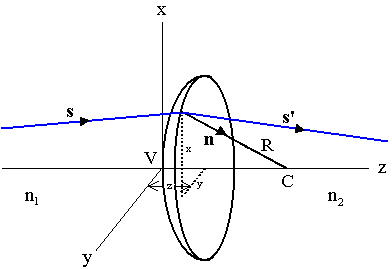
The general relation between s and s for the refracted ray is equation 3,
n2s = n1s + (n2cosθ2 - n1cosθ1)n.
This is a vector equation. In terms of the components along the axes of our coordinate system we may write
n2sx = n1sx + (n2cosθ2 - n1cosθ1)nx,
n2sy = n1sy + (n2cosθ2 - n1cosθ1)ny,
n2sz = n1sz + (n2cosθ2 - n1cosθ1)nz.
From geometry we have
nx = -x/R, ny = -y/R, nz = z/|R| = (R2 - x2 - y2)½/|R|.
At the interface we therefore have
n2sx = n1sx - (n2cosθ2 - n1cosθ1)x/R,
n2sy = n1sy - (n2cosθ2 - n1cosθ1)y/R,
n2sz = n1sz + (n2cosθ2 - n1cosθ1)(R2 - x2 - y2)½/|R|.
At the interface we also have
x = x,
y = y.
Since s·n = sxnx + syny +sznz = cosθ1, we can determine cosθ1 in terms of the Cartesian components of s and n and cosθ2 from the law of refraction.


After refraction at the interface, rays will travel in a straight line along the direction defined by s until they meet another interface. This linear propagation may be described by
x2 = x1 + (z2-z1)sx/sz,
y2 = y1 + (z2-z1)sy/sz.
These are the exact ray-tracing equations for refraction at a spherical interface.
![]()
Paraxial optics
Assume an optical axis can be defined, and all surface normals make small angles with this axis. Assume that all light rays also make small angles with the optical axis. Such rays are called paraxial rays. Let us now call θ1 and θ2 the angles a ray makes with the optical axis. If θ1 and θ2 are small, then cosθ1 ≈ 1, cosθ2 ≈ 1, and sinθ1 ≈ θ1, sinθ2 ≈ θ2. For paraxial rays sz = s cosθ1 ≈ 1, and sz = scosθ2 ≈ 1.
The ray tracing equations then become
n2sx = n1sx - (n2 - n1)x/R,
n2sy = n1sy - (n2 - n1)y/R,
for refraction at the spherical surface, and
x2 = x1 + (z2 - z1)sx,
y2 = y1 + (z2 - z1)sy.
for propagation through the homogeneous medium.
The equations for the projections of the rays on the xz-plane and on the yz-plane decouple and the projections can be treated independently.
Let us concentrate on the projections in the xz-plane. These projections behave as if the rays were actually lying in that plane. Rays that lie in a single plane containing the z-axis are called meridional rays. We now have a two-dimensional situation.
For refraction at a spherical surface we have
n2sx = n1sx - (n2 - n1)x/R,
x = x
and for propagation through a homogeneous medium we have
x2 = x1 + (z2 - z1)sx.
But
sx= s sinθ1 ≈ θ1, sx = s sinθ2 ≈ θ2.
Therefore we can write
n2θ2 = n1θ1 - (n2 - n1)x/R,
and
x2 = x1 + (z2 - z1)θ2.
These equations can be written in matrix form:
We have

for refraction, and
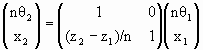
for propagation.
These transformations can be combined to give the overall transformation through several refracting and transmitting elements.
![]()