

An important part of the design of an optical system is its efficiency in transferring light. One must be able to specify the amount of energy emitted or received. For historical reasons, many similar quantities are used to specify the amount of light leaving the source or arriving at the receiver, and many different systems of units are used. Only in recent years has the situation improved with the gradual changeover to the International System of Units (SI).
To specify the amount of energy emitted by a source, we use the quantities.
| Energy | |
| Power | |
| Power per unit area | |
| Power per unit solid angle | |
| Power per unit solid angle per unit projected area |
To specify the amount of energy received by a detector, we use one quantity.
| Power per unit area |
A radian is the angle subtended at the center of a circle of radius r by a section of its circumference of length equal to r. Dividing 2πr by r gives 2π as the number of radians in a full circle.
A steradian is the solid angle subtended at the center of a sphere of radius r by a section of its surface area of magnitude equal to r2. Since the surface area is 4πr2, there are 4π steradians surrounding a point in space.
Let a cone of arbitrary shape have its apex at the center of a sphere of unit radius. The solid angle Ω at the apex is numerically equal to the surface area on the sphere intercepted by the cone, since the full sphere has an area of 4π.
![]()
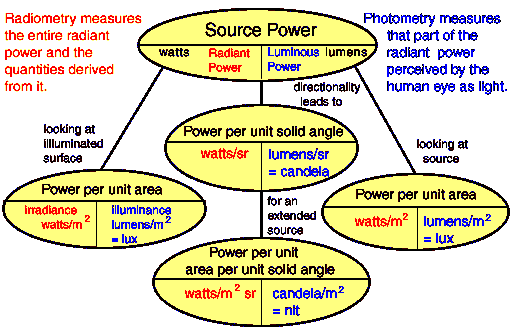
When specifying energy, power, power per unit area, power per unit solid angle, and power per unit solid angle per unit projected area, we can specify radiometric quantities, which apply to radiation of any wavelength, or photometric quantities, which only apply to visible light.
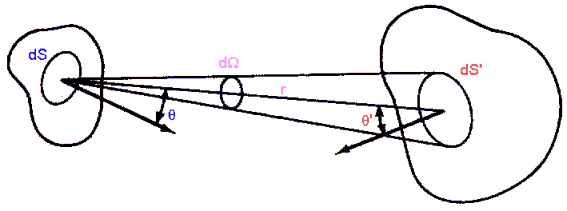
In the figure above, let the area dS be the source of electromagnetic radiation. The area dS emits radiation toward a receiving area dSí at a distance r.
Radiometric quantities
| In SI units, the energy E of the emitted radiation is measured in Joule (J). | |
| The radiometric power P = dE/dt = Φ emitted from a surface dS is called the radiant flux, and it is measured in J/s = Watt (W). | |
| The power per unit area dP/dS = M is called the radiant emittance. It is measured in W/m2. | |
| The power per unit solid angle dP/dΩ = I is called the radiant intensity. It is measured in unit of W/sr. It can have an angular dependence. We then specify I(θ). | |
| The power per unit solid angle per unit projected area is called the
radiance
L. It is measured in W/sr/m2. An important part of
the definition of L is the specification of the area. We use the
normal or projected area dS cosθ, since the
energy received at dSí depends not only on the size of dS but also on its
orientation. (The area is projected onto a plane whose normal is the line of
sight.) L = I/(dS cosθ) = d2P/(dΩ dS cosθ) | |
| The amount of energy received from a source by the surface dSí is the irradiance E, measured in W/m2. |
Photometric quantities
The corresponding photometric quantities are tied to the sensitivity of the human eye, our main detector for visible light.
In SI units, the energy of the emitted radiation is measured in Joule. However, if the wavelength of the emitted radiation lies in the 400ó700 nm range, i.e. the visible range, then the energy is called luminous energy and its unit is the Talbot.
| The photometric equivalent of the radiant flux Φ
is the luminous flux Φ, whose units are
lumens (lm).
The figure above shows the sensitivity of the eye as a function of wavelength or color. The peak is in the green at 555 nm. 1 W of green light is equivalent to 683 lm. | |
| The photometric equivalent of the radiant emittance M is the luminous emittance M, measured in lm/m2. | |
| The photometric equivalent of the radiant intensity I is the
luminous
intensity I. It is measured in lm/sr or candela. Candela was
once known as the candle. The luminous intensity I was called the
"candlepower". (A source with a uniform flux of 4π lm radiates 1 lm/sr or 1 candela. Hence, 4π or 12.57 lm of radiant flux from an isotropic source means that I = 1 cd. A typical 100-watt light bulb provides about 1,700 lm of visible energy. If the distribution were uniform, the luminous intensity I would be about 135 cd.) | |
| The photometric equivalent of the radiance L is the luminance L, measured in candela/m2 or lm/sr/m2. The luminance L is the property of a source that is commonly called "brightness". The unit for L used to be the Lambert. | |
| The photometric equivalent of the irradiance E is the illuminance E, measured in lm/m2 = lux (lx). |
![]()
If the energy supplied by dS is being received from another source and retransmitted isotropically, i.e. if dS is a perfect diffuser and its radiance or brightness is not a function of angle, then L = I/(dS cosθ) = I/dSn = constant and I(θ) = LdS cos(θ) is related to its normal component In by the equation
I(θ) = In cosθ.
This is known as Lambertís law. A surface which satisfies Lambertís law is called Lambertian. Lambertian refers to a flat radiating surface. (The flat surface can be an elemental area of a curved surface.) A Lambertian surface can be an active surface or a passive, reflective surface. The intensity I(θ) falls off as the cosine of the observation angle with respect to the surface normal (Lambert's law). The radiance (W/(m2sr)) is independent of direction. A good example is a surface painted with a good "matte" or "flat" white paint. If it is uniformly illuminated, like from the sun, it appears equally bright from whatever direction you view it.
|
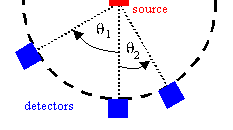
In the figure on the right, if the source is Lambertian and equally bright
in all directions, then the amount of energy that falls each the detectors is
not the same for each of the detectors, but depends on the angle θ
as cosθ. The apparent brightness of a Lambertian surface is the same when viewed from any angle. For a Lambertian surface only, we have the relation ship between the emittance M and the radiance L, M = πL. [L = d2P/(dΩ dS cosθ). If L is constant,
then The ratio of the radiant emittance (W/m2) to the radiance (W/m2sr) of a Lambertian surface is a factor of π and not 2π. The radiance is integrated over a hemisphere. The factor of cos(θ) in the definition of radiance is responsible for this result. It is counterintuitive, since there are 2π steradians in a hemisphere. |
 |
![]()
|
Problem: Consider a point P on a line normal to the center of a disk. The point is a distance a from the center of the disk, which has a radius R. (a) Show that the solid angle subtended by the disk at the point is
(b) Show that, when the point P is very far from the disk,
the solid angle reduces to zero. |
|
||
|
|
||
| Problem: A lens with a diameter of 1.25 in. and a focal length of 2.0 in. projects the image of a lamp capable of producing 3,000 cd/cm2. Find the illuminance E in lm/ft2 (footcandles) on a screen 20 ft from the lens.
|
|