

Consider a wave propagating through space. Coherence is a measure of the correlation that exists between the phases of the wave measured at different points. The coherence of a wave depends on the characteristics of its source.
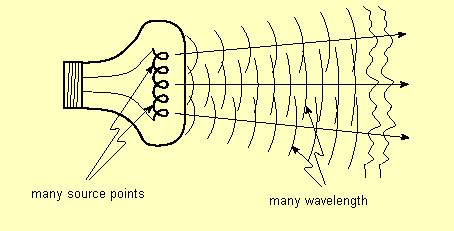
Let us look at a simple example. Imagine two corks bobbing up and down on a wavy water surface. Suppose the source of the water waves is a single stick moved harmonically in and out of the water, breaking the otherwise smooth water surface. There exists a perfect correlation between the motions of the two corks. They may not bop up and down exactly in phase, one may go up while the other one goes down, but the phase difference between the positions of the two corks is constant in time. We say that the source is perfectly coherent. A harmonically oscillating point source produces a perfectly coherent wave.
When we describe the coherence of light waves, we distinguish two types of coherence.
| Temporal coherence is a measure of the correlation between the phases of a
light wave at different points along the direction of propagation.
Temporal coherence tells us how monochromatic a source is.
Assume our source emits waves with wavelength λ ± Δλ. Waves with wavelength λ and λ + Δλ, which at some point in space constructively interfere, will no longer constructively interfere after some optical path length lc = λ2/(2πΔλ); lc is called the coherence length. [The phase of a wave propagating into the x-direction is given by
φ
= kx - ωt. Look at the wave pattern in
space at some time t. At some distance l the phase
difference between two waves with wave vectors k1 and k2
which are in phase at x = 0 becomes Δφ = (k1
- k2)l. When Δφ = 1, or Δφ ~ 60o, the light is no longer considered coherent.
Interference and diffraction patterns severely loose contrast. The wave pattern travels through space with speed c. lc = λ2/(2πΔλ) = λf/(2πΔf) = c/Δω, tc = 1/Δω. If we know the wavelength or frequency spread of a light source, we can calculate lc and tc. We cannot observe interference patterns produced by division of amplitude, such as thin-film interference, if the optical path difference greatly exceeds lc. | |
| Spatial coherence is a measure of the
correlation between the phases of a light wave at different points
transverse to the direction of propagation. Spatial coherence tells us how uniform the phase of the
wave front is.
A distance L from a thermal monochromatic (line) source whose linear dimensions are on the order of δ, two slits separated by a distance greater than dc = 0.16λL/δ will no longer produce a recognizable interference pattern. We call πdc2/4 the coherence area of the source. [At time t look at a source of width δ a perpendicular distance L from a screen. Look at two points (P1 and P2) on the screen separated by a distance d. The electric field at P1 and P2 is a superposition of the electric fields of the waves emitted by all source points, whose emissions are not correlated. In order for EM waves leaving P1 and P2 to produce a recognizable interference pattern, the superpositions at P1 and P2 must stay in phase. screen
source of width δ Light waves emitted from the two edges of the source have a some definite phase difference right in the center between the two points at some time t. A ray traveling from the left edge of δ to point P2 must travel a distance ~d(sinθ)/2 farther then a ray traveling to the center. The path of a ray traveling from the right edge of δ to point P2 travel is ~d(sinθ)/2 shorter then the path to the center. The path difference for the two rays therefore is dsinθ, which introduces a phase difference Δφ' = 2πdsinθ/λ. For the distance from P1 to P2 along the wave front we therefore get a phase difference Δφ = 2Δφ' = 4πdsinθ/λ. Wavelets emitted from the two edges of the source are that are in phase at P1 at time t are are out of phase by 4πdsinθ/λ at P2 at the same time t. We have sinθ ~ δ/(2L), so Δφ = 2πdδ/(Lλ). When Δφ = 1 or Δφ ~ 60o, the light is no longer considered coherent. Δφ = 1 --> d = Lλ/(2πδ) = 0.16 Lλ/δ.] |
An incandescent light bulb is an example of very incoherent source.
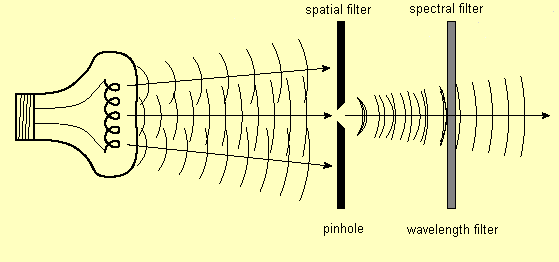
We can produce coherent light from an incoherent source if we are willing to throw away a lot of the light. We do this by first spatially filtering the light from the incoherent source to increase the spatial coherence, and then spectrally filtering the light to increase the temporal coherence.
![]()
A sinusoidal plane wave extends to infinity in space and time. It is perfectly coherent in space and time, its coherence length, coherence time, and coherence area are all infinite. All real waves are wave pulses, they last for a finite time interval and have finite extend perpendicular to their direction of propagation. They are mathematically described by non-periodic functions. We therefore have to learn how to analyze non-periodic functions to find the frequencies present in wave pulses to determine Δω and the coherence length.
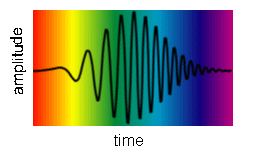
The light pulse in the figure above contains many frequencies. To determine the coherence length, we need to know its frequency content.
Any set of sinusoidal waves whose frequencies belong to a harmonic series will combine to produce a periodic complex wave, whose repetition frequency is that of the series fundamental. The individual components may have any amplitudes and any relative phases. These amplitudes and phases determine the shape of the complex waveform.
According to Fourier analysis, an arbitrary periodical waveform can be regarded as a superposition of sinusoidal waves. Fourier synthesis means superimposing many sinusoidal waves to obtain the arbitrary periodic waveform.
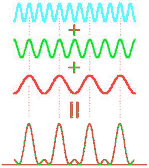
Any set of sinusoidal waves whose frequencies do not belong to a harmonic series will combine to produce a complex wave that is not periodic. Any non-periodic waveform may be built from a set of sinusoidal waves. Each component must have just the right amplitude and relative phase to produce the desired waveform.
Any piece-wise regular periodic function (finite # of discontinuities, finite # of extreme values) can be written as a series of imaginary exponentials. Assume f(t) is a periodic function of t with fundamental period T = 1/f.
f(t) = ∑-∞+∞Cnexp(iωnt)
Here ωn = n2πf, Δω = ωn+1 - ωn = 2πf. The coefficients Cm are given by
Cm = (1/T)∫0Tf(t)exp(-iωmt)dt.
Using eiωt = cos(ωt) + i sin(ωt) we can also write
f(t) = A0/2 + ∑n=1∞ Ancos(ωnt) + ∑n=1∞ Bnsin(ωnt)
with
A0 = (2/T)∫0Tf(t)dt
Am = (2/T)∫0Tf(t)cos(ωmt)dt
Bm = (2/T)∫0Tf(t)sin(ωmt)dt
We have An = (Cn + C-n), Bn = i(Cn - C-n), A0 = 2C0, n > 0.
Fourier's theorem states that any periodic function with period T (or spatial period or wavelength L) can be synthesized by a sum of harmonic functions whose periods (wavelengths) are integral submultiples of T (or L), such as T/2, T/3, ..., (or L/2, L/3, ...).
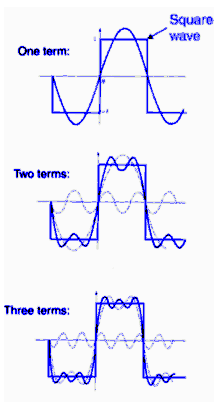
Synthesizing a square wave
Link:
The Fourier transform
In the limit T --> ∞ Fourier's theorem can be generalized to
f(t) =
(1/(2π)1/2)∫-∞+∞
f(ω)exp(iωt)dω
f(ω)
=
(1/(2π)1/2)∫-∞+∞
f(t)exp(-iωt)dt
Here f(t) and f(ω) are Fourier transforms of each other.
[Assume f(t) is a periodic function with period L.
f(t) = ∑-∞+∞ Cnexp(iωnt)
Cn = (1/T)∫0Tf(t)exp(-iωnt)dt =
(1/T)∫-T/2T/2f(t)exp(-iωnt)dt
Using Δω = 2πf, Δω/(2π) = f = 1/T, we write
Cn = (Δω/(2π))∫-T/2T/2f(t)exp(-iωnt)dt
f(t) = (1/(2π))∑-∞+∞exp(iωnt)Δω ∫-T/2T/2f(t')exp(-iωnt')dt'
As T --> ∞ , Δω --> 0, and this becomes
f(t) = (1/(2π))∫-∞+∞exp(iωnt)dω ∫-∞+∞f(t')exp(-iωnt')dt'
Defining f(ω) = (1/(2π)1/2)∫-∞+∞ f(t)exp(-iωt)dt
we have f(t) =
(1/(2π)1/2)∫-∞+∞
f(ω)exp(iωt)dω.]
Note: A Fourier transform is a linear transform;
f(t) = c1f1(t) + c2f2(t) implies f(ω) = c1f1(ω) + c2f2(ω) .

Examples:
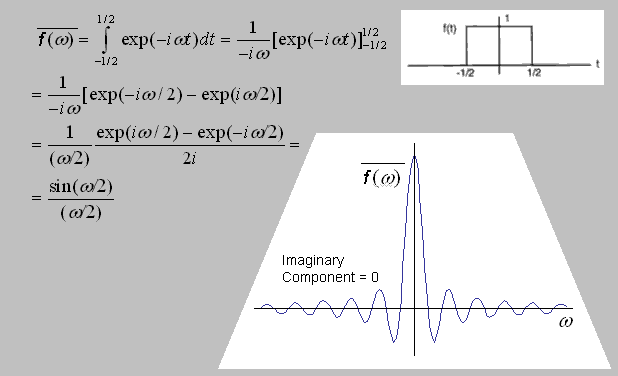
|
The Fourier transform of a rectangular pulse |
| The Fourier transform of a harmonic wave train of finite length. Let
f(t) = Aexp(iω0t), -T1/2 < t < T1/2. f(ω) = (1/(2π)1/2)∫-∞+∞ f(t)exp(-iωt)dt = (A/(2π)1/2)∫-T1/2T1/2 exp(-i(ω-ω0)t)dt
f(ω)
=
(A/((2π)1/2i(ω-ω0)))[exp(i(ω+ω0)(T1/2)) -
exp(-i(ω-ω0)(T1/2))] f(ω) is a representation of the wave train in frequency space. It gives the amplitudes and phases of the harmonic waves of all possible frequencies needed to synthesize the wave train. The function sin(x)/x = sinc(x) is called the sinc function.
While it is not zero for |x| > some number, we find that
it has a dominant peak between x = -π and x =
π with smaller fringes on
the sides. |
Uncertainty principle for wave packets:
ΔfΔt
~ 1.
The frequency bandwidth is of the same order as the reciprocal of the temporal
extend of the pulse.