The Fourier series

Any piece-wise regular periodic function (finite # of discontinuities, finite # of extreme values) can be written as a series of imaginary exponentials.
Assume f(x) is a periodic function of x with fundamental period L.

f(x) = ∑_-∞^+∞C_nexp(ik_nx)

Here k_n = n2π/L, Δk = k_n+1 - k_n = 2π/L.  The coefficients C_m are given by

C_m = (1/L)∫₀^L f(x)exp(-ik_mx)dx.

Using e^ikx = cos(kx) + i sin(kx) we can also write

f(x) = A₀/2 + ∑_n=1^∞ A_ncos(k_nx) + ∑_n=1^∞ B_nsin(k_nx)

with

A₀ = (2/L)∫₀^Lf(x)dx
A_m = (2/L)∫₀^Lf(x)cos(k_mx)dx
B_m = (2/L)∫₀^Lf(x)sin(k_mx)dx

We have A_n = (C_n + C_-n), B_n = i(C_n - C_-n), A₀ = 2C₀,  n > 0.

Fourier's theorem states that any periodic function with spatial period (wavelength) L can be synthesized by a sum of harmonic functions whose spatial periods (wavelengths) are integral submultiples of L, (such as L/2, L/3, ...).  In the limit  L --> ∞ Fourier's theorem can be generalized to

f(x) = (1/(2π)^1/2)∫_-∞^+∞ f(k)exp(ikx)dk 
f(k) = (1/(2π)^1/2)∫_-∞^+∞ f(x)exp(-ikx)dx

Here f(x) and f(k) are Fourier transforms of each other.

Show:

Assume f(x) is a periodic function with period L.

.

Using Δk = 2π/L,  Δk/2π = 1/L we write

.

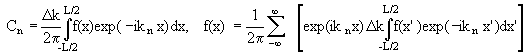As L --> ∞ , Δk --> 0 this becomes

.

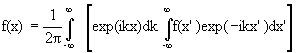Defining 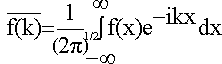, we have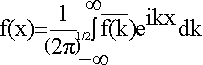

Note: A Fourier transform is a linear transform;

f(x) = c₁f₁(x) +c₂f₂(x)  implies  f(k) = c₁f₁(k) +c₂f₂(k) .