In this laboratory you will study the absorption of the decay products of Cesium 137 and Strontium 90 in different materials.

Background information:

Radioactive decay is a random process.  We cannot predict exactly when a certain unstable nucleus will decay, we can only predict the probability that the nucleus will decay in a certain time interval.  For a large sample, the decay rate is approximately R = R₀exp(-t/τ).   If the mean life τ is very large and we make measurements for a time interval t << τ, then during that time interval the decay rate R is approximately constant.  R ~ R₀ = N₀/τ.

In this experiment radiation is produced at an approximately constant rate.  We let that radiation travel through materials of different mass thickness x_m.  The mass thickness of a material is measured in mass per unit area, for example g/cm².  It is just the thickness of the material (cm) times the density of the material (g/cm³).

Absorption of radiation is also a random process.  When a particle travels through a material, we cannot predict exactly how far it will penetrate and at which depth it will be absorbed, we can only predict the probability that the particle will travel through a certain distance ∆x of the material.

When a beam of N₀ particles crosses a layer of absorber of mass thickness x_m, the number of particles that emerge is given by

N = N₀ exp(-μ_mx_m).

Here μ_m is called the mass attenuation coefficient of the material.  The rate at which particles are removed from the beam is

dN/dx_m = -μ_mN.

x_m1/2 is the half-value for the mass thickness, and it is given by x_m1/2 = ln(2)/μ_m.

The two most dangerous fission products in nuclear wastes are Strontium-90 (Sr-90) and Cesium-137 (Cs-137).  Their half-life is long enough so one has to worry about storage of the materials but short enough so one has to worry about high radiation release.  The two types of radioactive nuclei account for about 98% of the radioactive hazard after 10 years of storage.  Both nuclei have similar half-lives of about a human generation.  Sr-90's half-life is 28 years and Cs-137's is 30 years.  This means that after storing these materials for 30 years, 50% of the nuclei will have transmuted into other elements.

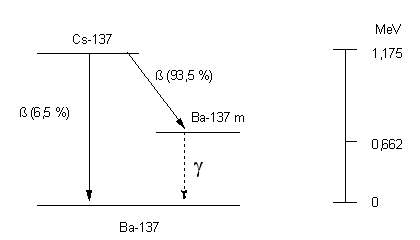
Cs-137 disintegrates with a probability of 6.5% directly and with a probability of 93.5% indirectly over the meta-stable barium-137m into stable barium-137.  During the indirect decay, beta rays having a maximum energy of 0.513 MeV are released.  The meta-stable Ba-137 changes into stable Ba-137 with a half-life of 2.55 minutes releasing a 0.662 MeV gamma ray.  The activity the Cs-137 is is deduced from the gamma rays.

Sr-90 beta-decays (0.546 MeV) into yttrium-90, which has a half-life of 64 hours.  Yttrium-90  beta-decays with a a probability of +99% directly into stable Zirconium-90 while emitting electrons with energies up to E_max = 2.27 MeV.  The activity of the Sr-90 is is deduced from the beta rays.

Equipment needed:

• Nucleus Scaler/Timer
• Geiger Tube with Stand and Source Holder
• Sr and Cs Radioactive Sources
• Lead and Polyethylene Absorber Set

Procedure:

Part 1:

You will measure x_m1/2, the half-value of the mass thickness, for 0.662 MeV gamma rays in lead.

• Download the linked spreadsheet and open it with Excel.  Go to sheet 1.
• Turn on the scaler.  Place it into stop mode by pressing the Stop and then the Reset switch.  Make sure the toggle switch is on Preset Time Minutes.  Choose 2 minutes for you preset counting time.
• Place the Cs-137 source into the fourth or fifth slot from the top of the source holder label side up.
• Put the #1 lead attenuator on a tray into the third or fourth slot from the top of the source holder.
• Press Reset, Count.  Record the number of counts after 2 minute in the spreadsheet.
• Repeat with all the combinations of lead attenuators listed in the spreadsheet.

Part 2:

You will measure x_m1/2, the half-value of the mass thickness, for E_max = 2.27 MeV beta rays from the decay of Sr-90 in polyethylene.

• Go to sheet 2 of the spreadsheet
• Place the Sr-90 source into the fourth or fifth slot from the top of the source holder label side up.
• Place the #3 polyethylene attenuator into the third or fourth slot from the top of the source holder
• Press Reset, Count.  Record the number of counts after 2 minute in the spreadsheet.
• Repeat with all the combinations of polyethylene attenuators listed in the spreadsheet.

Data Analysis:

Part 1:

• For all your measurement, calculate the # of counts per second and enter into column E of the spreadsheet.
• Now let Excel fit your data with the fitting function N = N₀ exp(-μ_mx_m) + b (background).
• Into cells B16, B17, and B19 type initial guesses for N₀, μ_m, and b.
• Into cell F5 enter the fitting function.  Enter the formula =B$16*EXP(-B$17*C5)+B$18.  Copy the formula down to row 13.
• Into column G enter the squares of the differences between your measured values and the fitting function.
• Into cell G5 enter the formula =(F5-E5)^2.  Copy the formula down to row 13.
• Into cell G14 enter the sum of these entries.  Enter the formula =SUM(G5:G13).
• On Excel's menu bar click Data, Solver.  If solver is not an option, click thee office button in the upper left corner, choose Excel Options, Add-Ins, Manage, and make sure Solver Add-in has a checkmark.
• Set target cell G14,  Equal to Min, by changing cells $B$16:$B$18, and click Solve.  Keep the solver solution.
• Solver adjusts the values  N₀, μ_m, and b (the entries in cells B17, B18 and B19) until the best fit is obtained.
• Produce a graph of your data (counts/s) and the fitting function versus mass thickness (g/cm²).
• The value in cell B17 is the value of μ_m you extracted from your data.  Calculate x_m1/2, the half-value of the mass thickness, for 0.662 MeV gamma rays in lead.

Part 2:

• Go to sheet 2 and repeat what you have done on sheet 1.
• In part 2 you calculate x_m1/2, the half-value of the mass thickness, for E_max = 2.27 MeV beta rays from the decay of Sr-90 in polyethylene.

Open Microsoft Word and prepare a report.

Name:
E-mail address:

Laboratory 9 Report

• Summarize the experiment.

• Insert your graphs.

• Discuss your results.  In the discussion you should answer the following questions:

  • Which value did you obtain for  x_m1/2, the half-value of the mass thickness, for 0.662 MeV gamma rays in lead?

  • Which value did you obtain for  x_m1/2, the half-value of the mass thickness, for E_max = 2.27 MeV beta rays from the decay of Sr-90 in polyethylene?

  • How do those two values compare?  How much more material is required to stop 50% of the gamma rays compared to 50% of the beta rays.

  • Which mass thickness of lead do you need to stop attenuate 99% of the gamma rays?  Given the density of lead, 11.3 g/cm³, what is the thickness of such a sheet of lead?

• Add any comments or questions you may have.