PDF with typeset equations

In this laboratory you will work with complex numbers.  You will plot complex numbers in the complex plane, convert complex numbers from rectangular to polar form and from polar to rectangular form and add, subtract, multiply and divide complex numbers.

• millimeter paper
• ruler and protractor
• calculator or Excel spreadsheet

Procedure:

Study the sections below and complete tasks 1-5.  Answer all questions highlighted in blue in full sentences.  Open a Microsoft Word document to keep a log of your answers.

Imaginary numbers
What number, when multiplied by itself gives (-1)?  The answer is none of the ordinary numbers.  This number, √(–1) is not one of the real numbers like 1, 2, 3, etc.  It belongs to a completely different system of numbers which we call imaginary numbers.  The number √(–1) is denoted by the letter i, and the square root of any negative number can be written as a real number times i.  For example

√(–9) = √(9*(–1)) = √9 * √(–1)= 3 * i

All numbers with a factor of i are imaginary.

• Task 1:
  Answer the following questions:
  What is the square root of 36?  What is the square root of -36?

Complex numbers
We can add together a real number and an imaginary number, such as (4 + 3i).  Such a mixture with both a real part (4) and an imaginary part (3i) is called a complex number.  These two parts are distinct, there is no way we can confuse the real and imaginary parts because imaginary numbers are not part of the real number system.  We can treat a complex number in the same way we handle a two dimensional coordinate vector, plotting the real and imaginary parts along different axes.  It is traditional to plot the real part along the x axis and the imaginary part along the y axis. Thus, for example, the complex number (4 + 3i) can be represented by a point whose coordinate vector has an x component of 4 and a y component of 3 as shown in the figure below.

Once we start plotting complex numbers on x and y axes, we will find that any complex number can be expressed in the exponential form

x + iy = r cos(φ) + i r sin(φ) = r exp(iφ).

Here exp(iφ) is defined as exp(iφ)= cos(φ) + i sin(φ).  When using the exponential notation, we give the angle in radians.

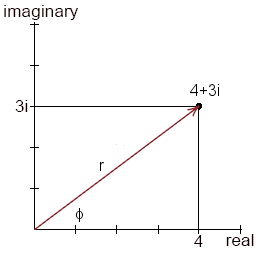
One way to describe the point  4 + 3i in the complex plane is to give its x and y coordinates (x = 4, y = 3i).  An equally good description, is to give the distance r from the origin to the point, and the angle φ that r makes with the x or real axis.  From the Pythagorean theorem we have

r² = x² + y² = 16 + 9 = 25,
r = 5.

The tangent of the angle φ is the opposite side y divided by the adjacent side x, tanφ = y/x = 3/4 = 0.75,  φ = 36.9°.  Thus the point 4 + 3i is located at a distance r = 5 from the origin at an angle φ = 36.9°.  It is traditional to use the letter z to describe a complex number.  Thus if a complex number (z) has a real part (x) and an imaginary part (iy), we can write,

z = x + iy = r cos(φ) + i r sin(φ),
z = r(cos(φ) + isin(φ)).

• Task 2:
  Let z = 6 + 8i.

  • Use millimeter paper, set up a coordinate system with a real and an imaginary axis, and plot the point z.  Label the point.

  • z = r(cos(φ) + isin(φ)).  Use a ruler and a protractor and find r and φ.  What are your values using this method?

  • Find r and φ algebraically.  What are your values using this method?

  Let z = 6 - 8i.

  • Plot this point z on the same graph as the previous point.  Label the point.

  • What are r and φ for this point?

  Let r = 4.24, φ = 225^o.

  • z = x + iy.  What are the values for x and y?

Let us study the function cos(φ) + i sin(φ) in more detail.  Let us first look at the derivative of cos(φ) + i sin(φ).
Since dcos(φ)/dφ  = – sin(φ)  and  dsin(φ)/dφ = cos(φ) we get

d(cos(φ)+ i sin(φ))/dφ  = – sin(φ) + i cos(φ)

Since (–1) = i², this can be written

d(cos(φ) + i sin(φ))/dφ = i²sin(φ) + i cos(φ) = i (cos(φ) + i sin(φ))
 

To express this result more formally, let us write f(φ) = cos(φ) + i sin(φ).  Then

df(φ)/dφ = i f(φ).

To within a constant (i), the function f(φ) is equal to its own derivative.  What function that you are already familiar with, behaves this way?  The exponential function! 
Recall that d(exp(ax))/dx = a exp(ax).
Thus if we replace x by φ and a by i , we get

d(exp(iφ))/dφ = i exp(iφ).

We see that the function cos(φ) + i sin(φ) and the function exp(iφ) obey the same rule for differentiation.  When two functions have the same derivatives, does that mean that they are the same functions?  It does, if we show that both functions start off with the same value for small values of φ.  Then as we increase φ, if both functions have the same derivative or slope, i.e. if they CHANGE in the same way, they must continue to be the same function for all values of φ.

We can verify this by doing a series expansion.

For small values of x the function exp(x) can be written as

exp(x) ~ 1 + x +  x²/2,

and the functions cos(x) and sin(x) can be written as

cos(x) ~ 1 - x²/2,    sin(x) ~ x.

This is shown in the graphs below.

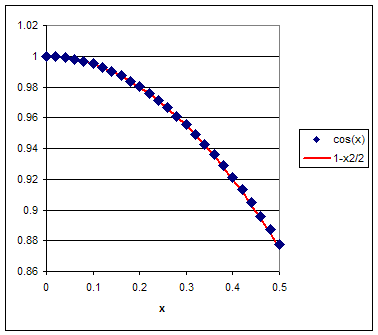
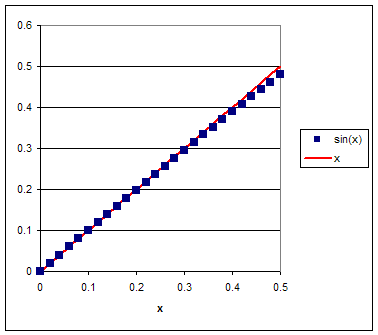
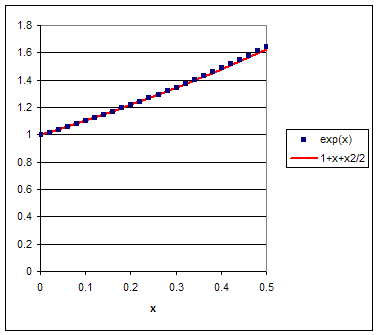
Therefore we can verify for small values of f that

exp(iφ) ~ 1 + iφ +  (iφ)²/2 = 1 + iφ -  φ²/2 = (1 - φ²/2) + iφ  = cos(φ) + i sin(φ).

So the function cos(φ) + i sin(φ) and the function exp(iφ) obey the same rule for differentiation and both functions start off with the same value for small values of φ.  Therefore we have for all values of φ

exp(iφ) = cos(φ) + i sin(φ).

If we replace φ by -φ we get exp(-iφ) = cos(-φ) + i sin(-φ). 
Since cos(-φ) = cos(φ)  sin(-φ) = –sin(φ), this gives

exp(-iφ) = cos(φ) - i sin(φ)

Adding exp(iφ) = cos(φ) + i sin(φ) and exp(-iφ) = cos(φ) - i sin(φ) we find

cos(φ) = (exp(iφ) + exp(-iφ))/2

and subtracting  we find

sin(φ) = (exp(iφ) - exp(-iφ))/(2i).

This gives us a complete prescription of how to go back and forth between cos(φ), sin(φ), and exp(iφ).
Finally returning to our complex function we write
 

z = x + iy = r cos(φ) + i r sin(φ) = r exp(iφ)). 

We have z =  r exp(iφ) as the other way of expressing a complex number, where r is the distance from the origin and φ the angle the coordinate vector r makes with the x or real axis.

• Task 3:
   Let z = 6 + 8i.
   
  • How do you write z in exponential form?

  Let z = 5 exp(i3.665)

  • z = x + iy. What are the values for x and y?

The complex conjugate z^*

The complex conjugate of a complex number is defined as the number we get by replacing all factors of i by –i in the formula for the number.  We generally denote the complex conjugate by placing an asterisk after the number.  For example, if z = x + iy, then z^* = x – iy.   If we start with z = r exp(iφ), then z^* = r exp(-iφ).

• Task 4:
  Let z = 5.3 - 4.2i.
   
  • Plot z and z^*.  Label the points

  Let z = 6 exp(i 5.585)

  • Plot z and z^*.  Label the points.

Adding, subtracting, multiplying and dividing complex numbers

Let z₁ = x₁ + iy₁, z₂ = x₂ + iy₂.

• Addition:
  If z = x + iy = z₁ + z₂, then x = x₁ + x₂ and y = y₁ + y₂.   The real parts and the imaginary parts do not mix.  We add the real parts and the imaginary parts separately.
   
• Subtraction:
  If z = x + iy = z₁ - z₂, then x = x₁ - x₂ and y = y₁ - y₂.   The real parts and the imaginary parts do not mix.  We subtract the real parts and the imaginary parts separately.
   
• Multiplication:
  Let z = z₁z₂.  z = (x₁ + iy₁)(x₂ + iy₂) = x₁x₂ + ix₁y₂ + iy₁x₂ – y₁y₂ = (x₁x₂ – y₁y₂) + i(x₁y₂ + y₁x₂).
  If z = x + iy, then x = x₁x₂ – y₁y₂, and y = x₁y₂ + y₁x₂.  Multiplication mixes the real and imaginary parts of the two numbers.

The main reason for defining a complex conjugate is that the product of a complex number z with its complex conjugate z* is always a real positive number, equal to the square of the distance r of the complex point from the origin.  For our two examples above, we have

z^*z = (x– iy)(x + iy) = x² – ixy + iyx – i²y² = x² + y² = r²

and

z^*z = r exp(iφ) r exp(-iφ) = r².

We call z*z  the square of the absolute value of the complex number and denote it by z^*z  = |z|².

• Division:
  Let z = z₁/z₂ = z₁z₂^*/(z₂z₂^*)  = z₁z₂^*/|z₂|².  We make the denominator real.
   z = (x₁ + iy₁)(x₂ - iy₂)/(x₂² + y₂²) = (x₁x₂ - ix₁y₂ + iy₁x₂ + y₁y₂)/(x₂² + y₂²)
  = [(x₁x₂ + y₁y₂) + i(-x₁y₂ + y₁x₂)]/(x₂² + y₂²) .
  If z = x + iy, then x = (x₁x₂ + y₁y₂)/(x₂² + y₂²)  and y = (-x₁y₂ + y₁x₂)/(x₂² + y₂²).  Division mixes the real and imaginary parts of the two numbers.
   
• Task 5:
  Let z₁ = 3 + 5i and z₂ = 7 - 4i.
   
  • What are the values of |z₁|² and |z₂|²?
  • What are the values of z = z₁ + z₂ and  z = z₁ - z₂?
  • What is the value of z = z₂z₁?
  • What are the values of z = z₁/z₂ and  z = z₂/z₁?

Use your log to prepare a report.

Name:
E-mail address:

Laboratory 3 Report

• Describe, in your own words, what complex numbers are.

• Give an algebraic expression which has no real solution.

• Enter your answers to the questions (in blue) from parts 1-5.

• It is generally accepted that the five most famous numbers in mathematics are 1, 0, e, i, and π.
  Construct an algebraic equations using as many of the five numbers as possible without the use of other numbers.
  Are you able to use all five numbers in an equation?
  Submit your equation that uses the most of these numbers.

Submit your word document and your plot to your lab instructor.