

In-class group activity 5
Find the Fourier transform of a wave pulse
Consider a wave pulse y(x, t) at t = 0. If we want to build this wave pulse by superimposing harmonic waves, we need waves with many different wave numbers k = 2π/λ or wavelength λ. Excel has a Fourier transform function. Given a pulse y(x), Excel calculates the amplitudes of the sine and cosine waves that are needed to synthesize this pulse. These amplitudes as a function wave numbers k = 2π/λ are the magnitude of the Fourier transform of the pulse y(x).
Open a Microsoft Word document to keep a log of your results and discussions.
Click here to examine the plots of four wave pulses and the magnitudes of the corresponding Fourier transforms calculated using Excel.
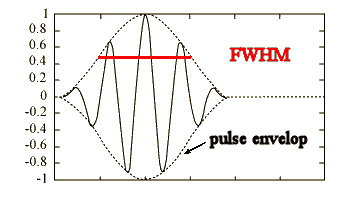
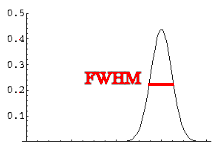
|
pulse |
∆x |
∆k |
product |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|