

In-class group activity 3
In this exercise you will explore the interference of two transverse harmonic waves of the form
y1 = A1sin(k1x - ω1t + φ1)
and
y2 = A2sin(k2x - ω2t + φ2).
You will use a Microsoft Excel spreadsheet. Sheet 1 has entries for the amplitudes, wavelengths, speeds, directions of travel, and phases of two sinusoidal waves. It has columns containing the position x, and the transverse displacement y of wave 1, wave 2, and their vector sum as a function of x at a given time. Sheet 2 shows a plot of the waveforms as a function of position x which can be animated. You will study the animated plot of the vector sum of the two waves for various combinations of amplitudes, wavelengths, speeds, directions of travel, and phases of wave 1 and wave 2.
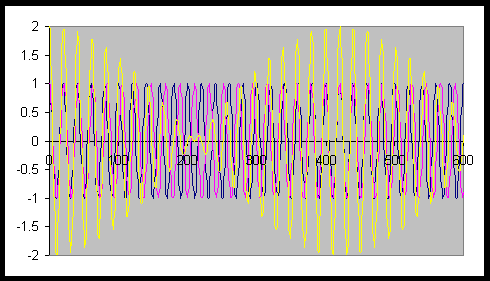
Beats occur when two wave have nearly, but not exactly, the same frequency. They are also the result of interference. Even though a crest may meet a trough at one instant in time at some point in space (destructive interference), at some later time at the same point a crest will meet a crest and the amplitudes will add (constructive interference). The frequency of the beats is equal to the difference in the frequencies of the two sound waves.
Save and then open the Microsoft Excel spreadsheet. Macros must be enabled.
Open a Microsoft Word document to keep a log of your results and conclusions.
wave1 |
wave2 |
|
amplitude |
1 |
1 |
wavelength |
2 |
2 |
speed |
1 |
1 |
phase |
0 |
0 |
direction |
1 |
1 |
Describe the animated graph of y1 + y2.
Look for constructive or destructive interference, a standing wave, or
beats? What do you observe?
wave1 |
wave2 |
|
amplitude |
1 |
1 |
wavelength |
2 |
2 |
speed |
1 |
1 |
phase |
0 |
0 |
direction |
1 |
-1 |
|
wave1 |
wave2 |
|
|
amplitude |
1 |
1 |
|
wavelength |
0.5 |
0.55 |
|
speed |
1 |
1 |
|
phase |
0 |
0 |
|
direction |
1 |
1 |
Describe the animated graph of y1
+ y2.
Look for constructive or destructive interference, a standing wave, or beats?
What do you observe?
When you add many waves with slightly different frequencies, you can build wave packets or wave pulses. Wave pulses can be viewed as the superposition of many harmonic (sinusoidal) waves with slightly different frequencies and phase constants.