Like all EM waves, light transports energy across space.  The intensity (energy per unit area and unit time) is proportional to the square of the amplitude of the electric field of the light wave.  This energy, however, arrives at a receiver not continuously but in discrete units called photons.  The energy transported by an electromagnetic wave is not continuously distributed over the wave front.  It is transported in discrete packages.  Photons are the particles of light.

Properties of photons:

• Photons always move with the speed of light.
• Photons are electrically neutral.
• Photons have no mass, but they have energy E = hf = hc/λ.  Here h = 6.626*10^-34 Js is a universal constant called Planck's constant.  The energy of each photon is inversely proportional to the wavelength of the associated EM wave.  The shorter the wavelength, the more energetic is the photon, the longer the wavelength, the less energetic is the photon.
  • A laser beam and a microwave beam can carry the same amount of energy.  In this case the laser beam contains a smaller number of photons, but each photon in the laser beam has a higher energy than the photons in the microwave beam.
• Photons can be created and destroyed.  When a source emits EM waves, photons are created.  When photons encounter matter, they may be absorbed and transfer their energy to the atoms and molecules. Creation and destruction of photons must conserve energy and momentum.  The magnitude of the momentum of a photon is p = hf/c = h/λ.

Problem:

• What is the energy of a photon of blue light (λ = 450 nm) and of a photon of red light (λ = 700 nm) in units of eV = 1.6*10^-19 J?

  Solution:
  E = hc/λ.
  Blue light: E = (6.626*10^-34 Js)(3*10⁸ m/s)/(450*10^-9 m) = 4.4*10^-19 J = 2.76 eV
  Red light: E = (6.626*10^-34 Js)(3*10⁸ m/s)/(700*10^-9 m) = 2.8*10^-19 J = 1.8 eV

Problem:

• A 100-W incandescent light bulb uses 100 W (100 W = 100 J/s) of electrical power but only radiates about 15 W of actual visible light.  Roughly how many visible photons per second hit the open pages of a typical hardcover book if the pages are about 2 m from the bulb and face it directly?
  • Solution:
    We have to make a variety of estimations and approximations to solve this problem.
    To find the number of photons hitting the pages each second, we have to know the light energy hitting the pages per second and the energy per photon.  We could compute the latter if we knew the wavelength of the light, but the visible light emitted by a normal incandescent bulb is a mix of wavelengths.
    Let us estimate that the average wavelength of the visible light is about 550 nm, which is in the yellow region of the spectrum.  This means that the average energy per photon is about

    E = hc/λ = (6.626*10^-34 Js)(3*10⁸ m/s)/(550*10^-9 m) = 3.61*10^-19 J = 2.26 eV.

    To find the number of photons hitting the pages of a book, we need to know the energy per second that falls on the pages.  Let us assume that the light energy from the bulb travels uniformly in all directions.  Imagine a sphere centered on the light bulb with a radius R = 2 m.  Every second, 15 J or so of visible light energy crosses this sphere.  If the light energy is spread uniformly over the sphere, then the intensity of the visible light or the energy per unit area per unit time in units of W/m² at any point on the inner surface of the sphere will be

    I = P_lamp/(4πR²),

    where P_lamp is the power of the visible light emitted by the lamp (~15 W) and 4πR² is the area of the inner surface of the sphere.

    I = (15/(16π))(W/m²)

    The book pages essentially lie on the inner surface of this imaginary sphere, they have area A.  The energy per unit time that falls on on this area is

    P_book = IA.
    (Energy per unit time falling on area A = energy per unit time per unit area times area A.)

    Taking a typical hardcover book and measuring it with a ruler, we find that the two facing pages form a rectangle about 18 cm tall and 24 cm wide, so A = (0.18 m)(0.24 m) = 0.058 m².  So

    P_book = (15/(16π))*0.058 W = 0.017 J/s.

    Finally, to find the number of photons per second falling on these pages, we have to divide P_book by the energy per photon.

    Number of visible photons from bulb hitting the book per second

    = (0.017 J/s)/(3.61*10^-19 J) = 4.7*10¹⁶/s.

    This is not an accurate number, but a useful, order of magnitude estimate.

In 1905, Einstein used the discrete nature of light to explain the photoelectric effect.  To demonstrate this effect light is shone on a metal surface.  If the frequency of the light is higher than the cutoff frequency f_c, then electrons are released.  No photoelectric electrons are emitted if the frequency of the light falls below this cutoff frequency f_c.  For many metal surfaces the frequency of blue light is greater than f_c and the frequency of red light is less than f_c.  If red light is shone on the surface, no electrons are emitted, no matter what the intensity of the light.  If blue light is shone on the surface, electrons are emitted.  The number of emitted electrons depends on the intensity of the light.  But even if the intensity is reduced to a very low value, electrons are still emitted, albeit at a very low rate.

The photoelectric effect cannot be understood within the wave picture of light.  To eject an electron from a metal surface a certain amount of energy Φ, called the work function of the metal, must be supplied to this electron.  In the wave picture the energy of the light beam does not depend on the frequency, but only on the intensity, which is proportional to the square of the amplitude.  Einstein explained the photoelectric effect by postulating that an electron can only receive the large amount of energy necessary to escape the metal from the EM wave by absorbing a single photon.  If this photon has enough energy, the electron is freed.  Excess energy appears as kinetic energy of the electron.  The maximum kinetic energy of the electron is given by E = hf - Φ.  If the photon does not have enough energy, then the electron cannot escape the metal.

Link:

• The photoelectric effect

Problems:

• Molybdenum has a work function of 4.2 eV.  Find the cutoff frequency and cutoff wavelength for the photoelectric effect.
  • Solution:
    hf_c = Φ,
    f_c = Φ/h = (4.2 eV)(1.6*10^-19 J/eV)/(6.626*10^-34 Js) = 1.01*10¹⁵ Hz is the cutoff frequency
    λ_c = c/f_c = 296 nm is the cutoff wavelength.
• Electrons are ejected from a metal surface with speeds ranging up to 4.6*10⁵ m/s when light with a wavelength of 625 nm is used.

  (a)  What is the work function of the surface?
  (b)  What is the cutoff frequency of the surface?

  • Solution:
    • (a)  Φ = hf - E.  E = (1/2)mv² = (1/2)(9.1*10^-31 kg)(4.6*10⁵ m/s)² = 9.63*10^-20 J
      hf = hc/λ = (6.626*10^-34Js)(3*10⁸ m/s)/(625*10^-9 m) = 3.18*10^-19 J
      Φ = (3.18*10^-19 J) - (3.18*10^-19 J) = 2.21*10^-19 J is the workfunction of the surface.
    • (b)  f_c = Φ/h = (2.21*10^-19 J)/(6.626*10^-34 Js) = 3.35*10¹⁴ Hz is the cutoff frequency.
• Light of wavelength 500 nm is incident on sodium with a work function of 2.28 eV.  What is the maximum kinetic energy of the ejected photoelectron?
  • Solution:
    E = hf - Φ = hc/λ - Φ.
    hf = hc/λ = (6.626*10^-34 Js)(3*10⁸ m/s)/(500*10^-9 m) = (3.98*10^-19 J)(1 eV)/(1.6*10^-19J) = 2.48 eV.
    E = 0.2 eV.

Link:

• The photoelectric effect applet

The Compton effect or Compton scattering (discovered in 1923, Nobel Prize in Physics in 1927) is another famous experiment supporting the existence of photons.  To observe the Compton effect, x-rays are scattered from (nearly) free electrons.  To understand Compton scattering we must think of photons as particles. 

Imagine an incoming photon scattering off a stationary electron.

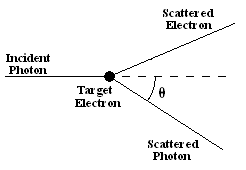
After the collision the photon's and the electron's trajectory will be at some angles with respect to the direction of the incoming photon.  If we know the energy and momentum of the incoming photon, and the angle the outgoing photon's trajectory makes with the direction of the incoming photon, then we can determine the outgoing photon's energy using energy and momentum conservation. 

The energy of a photon is E = hf = hc/λ and the momentum of the photon is p = hf/c = h/λ = E/c.
The relativistically correct expression for the energy of the electron is E_e = (p_e²c² + m_e²c⁴)^1/2.

The initial momentum of the electron is (nearly) zero.
Energy conservation requires E_i + E_ei = E_f + E_ef,  or  E_i + m_ec² = E_f + (p_ef²c² + m_e²c⁴)^1/2.
Momentum conservation requires p_i = p_f + p_ef.  This is a vector equation.
Rewriting these equations we have
(i)  (p_ef²c² + m_e²c⁴)^1/2 = E_i + m_ec² - E_f,
(ii)  p_ef² = p_ef•p_ef = (p_i - p_f)•(p_i - p_f) = p_i² + p_f² - 2p_i•p_f = p_i² + p_f² - 2p_ip_fcosθ,
where θ is the photon scattering angle.

Substituting (ii) into (i) and squaring we find
p_i² + p_f² - 2p_ip_fcosθ + m_e²c² = (E_i/c + m_ec - E_f/c)² = (p_i + m_ec - p_f)²
= p_i² + p_f² - 2p_ip_f + m_e²c² + 2(p_i - p_f)m_ec,
or
p_ip_f(1 - cosθ ) =  (p_i - p_f)m_ec,
(1 - cosθ)/(m_ec) = 1/p_f - 1/p_i.
It is traditional to rewrite this expression in terms of the change of the photon's wavelength.
Δλ = (λ_f - λ_i) = [h/(m_ec)](1 - cosθ).

The quantity h/(m_ec) = 0.00243 nm = 2.43 pm is called the Compton wavelength for photon-electron collisions.  The Compton wavelength is the amount by which the photon's wavelength changes when it scatters through 90°.  The change in wavelength is smaller if the scattering angle is less than 90°, and is a maximum of twice the Compton wavelength if the photon scatters backwards through 180°.  The Compton wavelength for photon-electron collisions is small (~10^-12 m) and the Compton effect is only observable with very short wavelength photons.  Only then does the change in the wavelength Δλ become an appreciable fraction of the wavelength λ.

Problem:

Photons of wavelength λ scatter elastically on free protons initially at rest.  By how much does the wavelength of the photons scattered at 90^o increase?

• Solution:
  Δλ = (λ_f - λ_i) = [h/(m_pc)](1 - cosθ), where m_p is the mass of the proton.
  For θ =90^o, Δλ =  h/(m_pc) = 1.32 fm

For photon-proton collisions the Compton wavelength is even smaller small (~10^-15 m) and the Compton effect is harder to measure and verify experimentally.