Three-dimensional problems

Two and three dimensional infinite square wells

The Schroedinger equation for a particle with mass m moving in two dimension has the form

 (-ħ2/(2m))[∂2ψ(x,y,t)/∂x2 + ∂2ψ(x,y,t)/∂y2] + U(x,y)ψ(x,y,t) = iħ∂ψ(x,y,t)/∂t,

and the Schroedinger equation for a particle with mass m moving in three dimension has the form

 (-ħ2/(2m))[∂2ψ(x,y,z,t)/∂x2 + ∂2ψ(x,y,z,t)/∂y2 + ∂2ψ(x,y,z,t)/∂z2] + U(x,y,z)ψ(x,y,z,t) = iħ∂ψ(x,y,z,t)/∂t.

If we want to solve this equation for eigenstates of the energy operator, we have to solve the equation

  (-ħ2/(2m))[∂2ψ(x,y)/∂x2 + ∂2ψ(x,y)/∂y2] + U(x,y)ψ(x,y) = Eψ(x,y)

in two dimensions, or the equation

 (-ħ2/(2m))[∂2ψ(x,y,z)/∂x2 + ∂2ψ(x,y,z)/∂y2 + ∂2ψ(x,y,z)/∂z2] + U(x,y,z)ψ(x,y,z) = Eψ(x,y,z)

in three dimensions.

We usually try to solve such equations by a technique called separation of variables.

Let us look at a particle trapped in a rectangular "infinite well".  The potential is 0 inside a rectangle with diagonal points of the origin and (Lx, Ly) and infinite outside the rectangle.

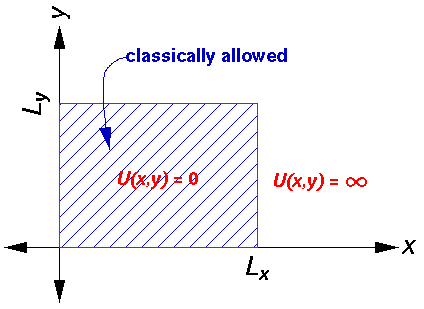
In the region where the potential is zero we solve the Schroedinger equation by trying a solution of the form

ψ(x,y) = φ(x)χ(y),

i.e. we write ψ(x,y) as a product of a function of x only and another function of y only.  This is called separation of variables.
We then have  (-ħ2/(2m))[∂2φ(x)χ(y)/∂x2 + ∂2φ(x)χ(y)/∂y2] = Eφ(x)χ(y).
All derivatives are partial derivatives.  When taking a partial derivative with respect to x, χ(y) is treated as a constant, and when taking a partial derivative with respect to y, φ(x) is treated as a constant.
We therefore have

(-ħ2/(2m))[χ(y)∂2φ(x)/∂x2 + φ(x)∂2χ(y)/∂y2] = Eφ(x)χ(y).

Dividing both sides by φ(x)χ(y) this equation can be rewritten as

(-ħ2/(2m))(1/φ(x))∂2φ(x)/∂x2 + (-ħ2/(2m))(1/χ(y))∂2χ(y)/∂y2 = E.

The first term in the sum on the left-hand side depends only on x and the second term only on y.  When we vary x, the second term is constant and the sum of the two terms is constant.  This implies that the first term also has to be equal to a constant.  We call this constant Ex.
When we vary y, the first term is constant and the sum of the two terms is constant.  This implies that the second term also has to be equal to a constant.  We call this constant Ey.
Using this approach we find that φ(x) is a solution of

(-ħ2/(2m))∂2φ(x)/∂x2  = Exφ(x),

and χ(y) is a solution of

(-ħ2/(2m))∂2χ(y)/∂y2  = Eyχ(y), 

and

E = Ex + Ey.

We have already solved these differential equations. (The same equations have the same solutions.)

φn(x,t) = (2/Lx)1/2sin(nxπx/Lx)exp(-iEnxt/ħ),   χn(y,t) = (2/Ly)1/2sin(nyπy/Ly)exp(-iEnyt/ħ),
Enx = nx2π2ħ2/(2mLx2),  nx = 1, 2, 3, ... ,  , Eny = ny2π2ħ2/(2mLy2),  ny = 1, 2, 3, ... .

For Lx = Ly = L, i.e. a two-dimensional square well,  we have  E = (nx2 + ny2)π2ħ2/(2mL2).

What is new?

We now can have energy degeneracy, two different eigenstates can have the same energy.

Example:

If two eigenstates have the same energy, then any linear combination of these eigenstates is also an eigenstate.  The stationary states are no longer unique.  A single energy measurement no longer defines the wave function uniquely.  To prepare a unique wave function we need to make a second measurement of another observable that can be measured simultaneously with the energy and whose eigenfunctions are unique combinations of energy eigenfunctions with the same energy.

Problem:

An electron is trapped in a two-dimensional, infinite rectangular well of width Lx = 800 pm and Ly = 1200 pm.  What is the electron's ground state energy?

To explore more features of particles in two-dimensional wells, you can follow the links below.

Links:

For the three dimensional infinite square well we try separation of variables and write ψ(x,y,z) = φ(x)χ(y)ζ(z). 
We then have to solve  (-ħ2/(2m))[∂2φ(x)χ(y)ζ(z)/∂x2 + ∂2φ(x)χ(y)ζ(z)/∂y2 + ∂2φ(x)χ(y)ζ(z)/∂z2] = Eφ(x)χ(y)ζ(z).
This separates into three equations,

(-ħ2/(2m))∂2φ(x)/∂x2  = Exφ(x),

(-ħ2/(2m))∂2χ(y)/∂y2  = Eyχ(y), 

(-ħ2/(2m))∂2ζ(z)/∂z2  = Eyζ(z), 

with E = Ex + Ey + Ez.
The three-dimensional square well is often used to model electrons trapped in a metal.  The electrons are free to move inside the metal, but are not allowed to escape from the metal in this simple model.