How do we interpret the wave function and how do extract information from the it?

PDF with typeset equations

The wave function, at a particular time, contains all the information that anybody at that time can have about the particle.  But the wave function itself has no physical interpretation.  It is not measurable.  However, the square of the absolute value of the wave function has a physical interpretation.  We interpret |ψ(x,t)|² as a probability density, a probability per unit length of finding the particle at a time t at position x.

The probability of finding the particle at time t in an interval ∆x about the position x is proportional to |ψ(x,t)|²∆x.

This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.  For the probability interpretation to make sense, the wave function must satisfy certain conditions.  We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.  We therefore require:

• The wave function must be single valued and continuous. The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1.

  Examples:

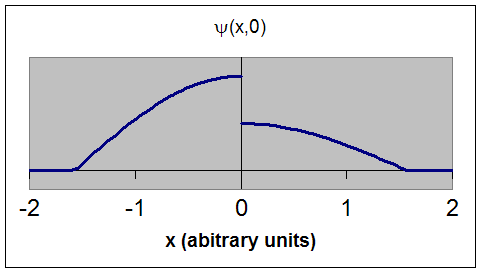  This is an acceptable wave function.  It is single valued and continuous.	This is an unacceptable wave function.  ψ(x,0) does not have a unique single value at x = 0.  The wave function is not continuous.

  The wave functions above are plotted at t = 0.  We have chosen wave functions whose imaginary part is zero at t = 0, so that ψ(x,0) is a real function that can be plotted easily.

• We must be able to normalize the wave function.  We must be able to choose an arbitrary multiplicative constant in such a way, so that if we sum up all possible values ∑|ψ(x_i,t)|²∆x_i  we must obtain 1.  The total probability of finding the particle anywhere must be one.  (The area under the curve |ψ(x_i,t)|² must 1.)
  [We really must evaluate that sum in the limit that ∆x_i goes to zero. 
  We write ∑_∆x-->0|ψ(x_i,t)|²∆x_i = ∫_-∞^+∞|ψ(x,t)|²dx = 1.  The sum becomes an integral.]

In-class activity: Normalize a wave function using a spreadsheet

Questions:

• Is the plane wave ψ(x,t) = Aexp(i(kx - ωt)) a wave function that satisfies the above requirements?
  ψ(x,t) = Aexp(i(kx - ωt)) is certainly a single valued and continuous function.  But what about normalization?

  The plane wave extents from -∞ to +∞.  The square of the absolute value at any point x is Aexp(i(kx - ωt))*Aexp(-i(kx - ωt)) = A².
  (A can be a complex number, but here we choose it to be real.)

  |ψ(x,t)|²∆x = A²∆x is a constant.

  But if we sum over all possible position intervals from -∞ to +∞ we obtain infinity unless A = 0.  So we get no position information.  The momentum of the particle described by ψ(x,t) = Aexp(i(kx - ωt)) is exactly known and therefore the uncertainty principle prevents us from making any predictions about its position.
   

• What is ψ(x,t) for a particular situation?

  Which superposition of plane waves gives us the correct wave function for a particular situation?

  Assume we make a measurement at t = 0 and find the particle in a small interval ∆x about x₁.  We then know that

  |ψ(x₁,0)|²∆x = 1 and |ψ(x ≠ x₁,0)|²∆x = 0. 

  We know then which wave packet we have to build and therefore can figure out which superposition of plane waves to us.  We always can determine which wave function to use by making a measurement.  The Schroedinger equation then predicts how this wave function evolves until we make a new measurement.

The most widely used interpretation of the wave function in quantum mechanics is given below:

Quantum mechanics is our current model of the microscopic world.  Like all models, it is created by people for people.

• Quantum mechanics divides the world into two parts, commonly called the system and the observer.

• The system is the part of the world that is being modeled.

• The rest of the world is the observer.

• An interaction between the observer and the system is called a measurement.

• Properties of the system that can be measured are called observables.  Examples are position, momentum, angular momentum, energy, etc.)

• The initial information the observer has about the system comes from a set of measurements.  (This is the same as in classical physics.)

• The state of the system represents this information, which can be cast into different mathematical forms.

• It is often represented in terms of a wave function.

• Quantum mechanics predicts how the state of the system evolves and therefore how the information the observer has about the system evolves with time.  Some information is retained, and some is lost.  The evolution of the state is deterministic.  The Schroedinger equation describes this evolution.  Measurements at a later time provide new information, and therefore the state of the system, in general, changes after the measurements.  The wave function of the system, in general, changes after a measurement.

So quantum mechanics does not really describe the system, but the information that the rest of the world can possibly have about the system.

The wave function has no direct physical meaning.  It is just one way of storing information.  It stores all the information available to the observer about the system.  To make predictions about the outcome of all measurements, at any time, one has to "do" something to the wave function to extract information.  One has to perform some mathematical operation on it, such a squaring it, multiplying it by a constant, differentiating it, etc.  One has to operate on the wave function with some operator.  (The operator is a specific instruction or set of instructions.)  Every observable is associated with its own operator.