Photons are the particles of light. Matter is made of atoms, and atoms are made protons, neutrons and electrons. These are not macroscopic particles. Typical atomic dimensions are on the order of 10-10 m, nuclear dimensions are on the order of 10-15 m, and the electron seems to be a point particle with no size at all. How do these particles behave?
If a wave equation describes the behavior of photons, maybe a wave equation also describes the behavior of other microscopic particles.
In 1924, Luis deBroglie (Nobel Prize in Physics in 1929) proposed that a wave function is associated with all particles. Where this wave function has nonzero amplitude, we are likely to find the particle. The standard interpretation is that the intensity of the wave function of a particle at any point is proportional to the probability of finding the particle at that point. The wavelengths of the harmonic waves used to build the wave function let us calculate the most likely momentum of the particle and the uncertainty in the momentum. The wave function for a material particle is often called a matter wave.
The relationship between momentum and wavelength for matter waves is given by p = h/λ, and the relationship energy and frequency is E = hf. The wavelength λ = h/p is called the de Broglie wavelength, and the relations λ = h/p and f = E/h are called the de Broglie relations. These are the same relations we have for the photon, but for particle E = (1/2)mv2 = p2/(2m), so E = ћ2k2/(2m), λ = h/√(2mE). The relationship between λ and E is different for particles than for photons.
A spread in wavelengths means an uncertainty in the momentum. The uncertainty principle also holds for material particles. The minimum value for the product ∆x ∆p is on the order of ħ.
∆x∆p ~ ħ.
For any particle, we cannot predict its position and momentum with absolute certainty. The product of the uncertainties is on the order of h/2π = ħ or greater.
A free particle of mass m moving with exactly determined velocity v in the positive x-direction has momentum p = mv, pointing into the positive x-direction and kinetic energy E = p2/(2m). Its wave function, which often is denoted by ψ(x,t), is a plane wave.
ψ(x,t) = Acos(kx - ωt + φ)
[The wave function is actually a complex function, and Acos(kx - ωt + φ) is the real part of this function. We will learn about complex functions in the next section.]
The wave function has a well defined deBroglie
wavelength λ
= h/p which determines k = 2π/λ.
The wave function also has a well defined deBroglie frequency f = E/h, which
determines the angular frequency ω
= 2πf.
Problem:
Problem:
Problem:
Think about:
If a particle is described by a plane wave ψ(x,t) = Acos(kx - ωt + φ) we know the particles momentum and wavelength exactly, but its position is completely unknown. The plane wave extends to infinity, the particle could be anywhere. The wave function for a particle for which we have some position information is a wave packet, and the particle's momentum now has some uncertainty.
Link: Wave packet Explorer
The more massive the particle, the larger is the magnitude of the momentum p of the particle when it is moving with speed v, and the smaller is the deBroglie wavelength λ. Wave packets build from harmonic waves with smaller wavelength can be smaller in size. The smallest wave packet we can build has a size on the order of the deBroglie wavelength λ of a free particle moving with the same speed v.
Example:
When we synthesized a square pulse with a width of 100 units using harmonic waves, the longest wavelength we used λ = 200 units.
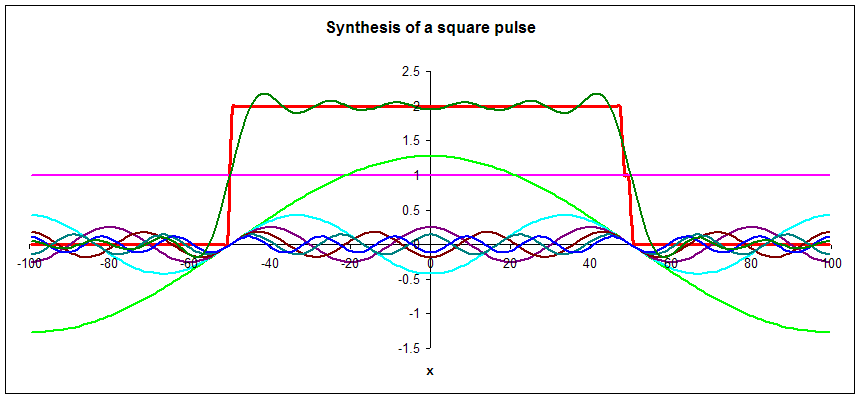
We can know the position of more massive particles moving with approximate speed v more precisely than the position of less massive particle moving with the same speed since the more massive particles have shorter deBroglie wavelengths.
Problem:
Assume we want to locate an
object with an uncertainty on the order of 1 Å, (1 Å (Angstrom) = 10-10
m, the approximate size of an atom).
What is the uncertainty in the speed of the object if the object is
(a) an electron (m = 9.1*10-31 kg),
(b) a proton (m = 1.67*10-27 kg),
(c) an uranium nucleus (m = 3.9*10-25 kg),
(d) a dust particle (m = 10-14 kg)?
Solution:
∆x = 10-10 m.
∆p = ħ/10-10 m = 10-24
kgm/s, ∆v = (10-24 kgm/s)/(mass
of particle)
(a) ∆v = (10-24
kgm/s)/(9.1*10-31 kg) = 1.1 106 m/s
So if we want to put an electron into a box the size of an atom, the
electron must be zipping around in that box, and its speed can be as
large as ~1 million meters per second. Electrons are confined in
atoms. The uncertainty principle tells us that they cannot be
sitting still, but must be moving around with high speeds.
(b) ∆v = (10-24
kgm/s)/1.67*10-27kg) = 6*102 m/s
(b) ∆v = (10-24
kgm/s)/(3.9*10-25 kg) = 2.6 m/s
(d) ∆v = (10-24
kgm/s)/(10-14 kg) = 10-10
m/s
For a dust particle the uncertainty in the speed is approximately 1 Å/s
or one atomic size/s. It must be jittering around a bit, but there
are few instruments capable of detecting this jitter.
As we increase the mass of the object further, the uncertainty in the
speed of the object becomes completely negligible.
So while the uncertainty
principle also holds for massive, macroscopic particles, it has no practical
consequences.
Photons always move with the speed of light c.
Monochromatic EM plane wave are of the form E(x,t)
= Emaxcos(kx
- ωt
+ φ)
= Emaxcos((2π/λ)x
- (2πf)t
+ φ).
They all have speed ω/k
=
2πf/(2π/λ)
= λf = c. If we
build a wave packet from plane waves of the above form, the speed of the wave
packet is c.
This relationship between ω
and k, ω = ck, is
called the dispersion relation
for photons in free space.
Particles can move with any speed. The plane matter waves of a free
particle moving with speed v has the form ψ(x,t)
= Acos(kx
- ωt
+ φ).
This wave function has a well defined wavelength
λ
= h/p and a well defined frequency f = E/h.
We have p = h/λ
=
ħk and
E =
hf = ħω.
But for a free particle we also have E = mv2/2 = p2/(2m)
= ħ2k2/(2m).
Equating the two expressions for E, we find
the relationship ω
= ħk2/(2m). This relationship
is called the dispersion relation for free
particles.
For any wave λf = ω/k = vwave. Using the dispersion relation for a free particle we find vwave = ω/k = ħk/(2m) = p/(2m) = mv/(2m) = v/2.
This may seem surprising. Our classical intuition suggests that a wave describing a particle moving with speed v should move with speed v itself. How else can it track the particle? But remember! If a particle is described by a plane wave ψ(x,t) = Acos(kx - ωt + φ) we know the particles momentum and wavelength exactly, but its position is completely unknown. It is impossible to track a particle whose momentum is exactly known.
The dispersion relation for free particles implies that the plane matter waves of particles do not all have the same speed. The wave function for a particle for which we have some position information is a wave packet. We have to superimpose plane waves describing particles with slightly different momenta and energies, or with slightly different wavelengths and frequencies. But these component waves now all move with slightly different speeds. So what happens to the shape of a wave packet as time goes on?
Let us investigate using a spreadsheet. We have previously built a square wave packets at t = 0 from sinusoidal waves with different wavelengths λl or different wave numbers k.
p = ħk, E = p2/2m = (ħk)2/(2m), ω = E/ħ = ħk2/(2m)
We will now let each of these waves move with
speed ω/k = vwave.
(We change the expression for each wave from ψ(x,t)
= Acos(kx) to ψ(x,t)
= Acos(kx - (ħk2/(2m))t)
in the spreadsheet. We choose units of 10-12 m = pm for length and 10-18 s
for time. For the mass of the particle we choose m = 10-30 kg,
approximately the mass of the electron.
Spreadsheet: A moving square pulse
The spreadsheets shows the moving wave packet and the dominant component wave.
We observe the wave packet changing shape as time progresses. We also
observe that the wave packet travels with a higher speed than the component
wave. The most likely speed of the particle is the speed of the center
of the wave packet. This speed is approximately twice the speed of the
component waves. If at some time we have located the particle with some
uncertainty ∆x, the minimum uncertainty
∆p in the momentum of the particle required by the
uncertainty principle implies greater and greater uncertainty in the position as
time progresses.
The speed of the plane waves making up a wave packet is called the phase velocity, vp = ω/k. The speed of a wave packet build using those plane waves is called the group velocity and is calculated using vg = dω/dk.
|
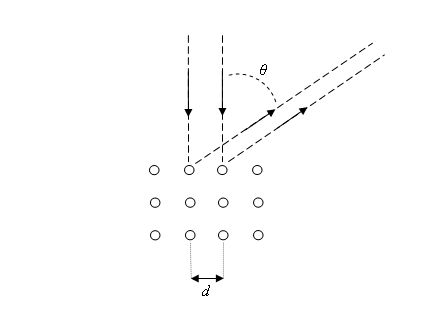
The first experimental verification of de Broglie's hypothesis came from two physicists working at Bell Laboratories in the USA in 1926. They scattered electrons off Nickel crystals and noticed that the electrons were more likely to appear at certain angles than others. The work was carried out by Clinton Davisson and Lester Germer. The Davisson-Germer apparatus is a vacuum glass tube which has in its interior an accelerator of electrons, a known crystal structured substance as a target and an electron detector. The figure on the right shows a simplified sketch of the experimental setup. This simple apparatus send an electron beam with an adjustable energy to a crystal surface, and then measures the current of electrons detected at a particular scattering angle theta.
|
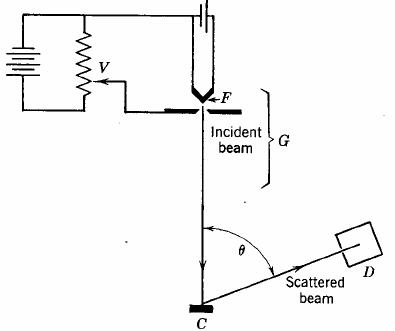 |
| The electron beam struck a
crystal target and was diffracted.
The experiment showed that constructive interference occurred at scattering angles satisfying the condition d sinθ = nλ with λ = h/p. The kinetic energy of the electrons accelerated through a potential difference (voltage) V was E = ½mv2 = p2/(2m) = eV and the de Broglie formula then yields λ = h/(2meV)1/2, where e and m are the charge and the mass of the electron respectively. Link: Powder diffraction |
 |
|
In the early 1960s it was possible to do an actual two-slit interference experiment with electrons. The experiment was done by C. H. Jönsson who created slits in copper foil about 0.5 micrometer in width and spaced 1 to 2 micrometer apart. The electrons had a kinetic energy of 50 keV and the interference pattern was displayed on a screen 35 cm from the slits. To make the pattern visible Jönsson employed a clever scheme of electrostatic lenses to magnify the image of the interference pattern. The figure on the right shows a simulation of the experiment and the predicted pattern
|

|