

In three dimensions we often encounter spherically symmetric potential energy functions. For example the potential energy of the electron in the hydrogen atom is the electrostatic potential energy of the proton-electron system. It depends only on the distance r of the electron from the proton, not on the direction of the position vector r. For the proton-electron system we have U(r) = -q2/(4πε0r) where q is the magnitude of the charge of the proton and the electron, q = 1.6 *10-19 C, and ε0 = 8.85*10-12C2/(Nm2) is a constant called the permittivity of free space. We put the origin of our coordinate system at the position of the proton.
Let us assume that U(x,y,z) = U(r). This means that the potential energy of the particle depends only on its distance from the origin. For such a potential, rectangular coordinates (x,y,z) are an inconvenient choice. Spherical coordinates are a much better fit. Spherical coordinates are defined in the figure below. We specify a position r, by giving its distance r from the origin, the angle θ the position vector makes with the z-axis, and the angle φ the projection of the position vector onto the x-y plane makes with the x-axis.
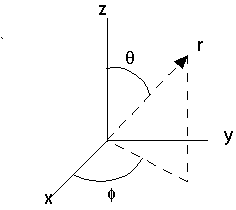
The relationships between spherical coordinates ad rectangular coordinates are
z = r cosθ, y = r sinθ sinφ, x = r sinθ cosφ, (0 < r < ∞, 0 < θ < π, 0 < φ < 2π),
or
r = ( x2 + y2 + z2)1/2, tanθ = ( x2 + y2)1/2/z, tanφ = y/x.
Problems:
Find the spherical coordinate defining the point x = 1, y = 1, z = 1.
Find the rectangular coordinates of a point defined by r = 2, θ = 30o, φ = 180o.
The time-independent Schroedinger equation for a particle moving in a spherically symmetric potential with potential energy U(r) = U((x2+y2+z2)1/2) is
(-ħ2/(2m))[∂2ψ(x,y,z)/∂x2 + ∂2ψ(x,y,z)/∂y2 + ∂2ψ(x,y,z)/∂z2] + U((x2+y2+z2)1/2)ψ(x,y,z) = Eψ(x,y,z)
In spherical coordinates it is written as
(-ħ2/(2m))[(1/r)∂2(rψ(r,θ,φ))/∂r2
+ (1/(r2sinθ))∂(sinθ ∂ψ(r,θ,φ)/∂θ)/∂θ
+ (1/(r2sin2θ))∂2ψ(r,θ,φ)/∂φ2]
+ U(r)ψ(r,θ,φ) = Eψ(r,θ,φ)),
since
∂2ψ/∂x2 + ∂2ψ/∂y2 + ∂2ψ/∂z2 = (1/r)∂2(rψ)/∂r2 + (1/(r2sinθ))∂(sinθ ∂ψ/∂θ)/∂θ + (1/(r2sin2θ))∂2ψ/∂φ2.
In spherical coordinates separation of variables is possible. We write ψ(x,y,z) = R(r) Θ(θ) Φ(φ) and find
(-ħ2/(2m))[(1/(Rr)∂2(rR))/∂r2 + (1/(Θr2sinθ))∂(sinθ∂Θ/∂θ)/∂θ + (1/(Φr2sin2θ))∂2Φ/∂φ2] = E - U(r),
or
(r2/(Rr)∂2(rR))/∂r2 + (2mr2/ħ2)(E - U(r)) + (1/(Θsinθ))∂(sinθ∂Θ/∂θ)/∂θ + (1/(Φsin2θ))∂2Φ/∂φ2 = 0.
The first term in the sum depends only on r and the second only on the angles θ and φ. Each term must be equal to a constant, and the two constants must sum to zero. We write
(r2/(Rr)∂2(rR))/∂r2
+ (2mr2/ħ2)(E - U(r)) = k,
(1/(Θsinθ))∂(sinθ∂Θ/∂θ)/∂θ
+ (1/(Φsin2θ))∂2Φ/∂φ2
= -k.
The second equation can then be rewritten as
sinθ(1/Θ)∂(sinθ∂Θ/∂θ)/∂θ + ksin2θ + (1/Φ)∂2Φ/∂φ2 = 0.
The first term in the sum depends only on θ and the second only on φ. Each term must be equal to a constant, and the two constants must sum to zero. We write
sinθ(1/Θ)∂(sinθ∂Θ/∂θ)/∂θ + ksin2θ = m2,
and
(1/Φ)∂2Φ/∂φ2 = -m2, ∂2Φ/∂φ2 = -m2Φ, Φm(φ) = Aexp(imφ).
Since Φm(φ)
must be periodic with period 2π, we need m to be an
integer, m = 0, ±1, ±2, ... .
The functions A exp(imφ) are eigenfunctions of
the operator (ħ/i)∂/∂φ,
which is the operator for the z-component of the orbital
angular momentum, Lz.
Its eigenvalues are mħ, the z-component of the
angular momentum is quantized.
The equation (1/(sinθ))∂(sinθ∂Θ/∂θ)/∂θ + (k - m2/sin2θ)Θ = 0, with m equal to an integer has acceptable solutions in the region 0 < θ < π if k = l(l + 1) and |m| ≤ l. We denote these functions by Θl(θ) and the product of the functions Θl(θ)Φm(φ) by Ylm(θ,φ).
The Ylm(θ,φ) are eigenfunctions of the operator L2 = (ħ2/(sinθ))∂(sinθ∂/∂θ)/∂θ + (ħ2/(sin2θ))∂2/∂φ2, which is the operator for the square of the magnitude of the orbital angular momentum. Its eigenvalues are l(l + 1)ħ2. The square of the magnitude of the orbital angular momentum is quantized.
The radial equation now becomes (-ħ2/(2m))∂2(rR))/∂r2 + (l(l + 1)ħ2/(2mr2))(rR) = (E - U(r))(rR). The solutions Rnl(r) to this equation depend on the exact form of the potential energy function U(r).
In spherical coordinated each solution of the time independent Schroedinger equation with U(x,y,z) = U(r) can be written as as a product of a function that depends only on r, and another function that depends on the angles θ and φ. We write
ψnlm(r,θ,φ) = Rnl(r)Ylm(θ,φ).
Different quantum numbers n, l, and m denote different stationary states. (In three dimensions we need three quantum numbers.) The eigenstates of the energy operator are also eigenstates of the square of the angular momentum operator, L2, and of the z-component of the angular momentum operator, Lz. The quantum number l characterizes the eigenvalues of L2, and the quantum number m characterizes the eigenvalues of Lz. E, L2 and Lz are compatible observables for a particle with potential energy U(r), we can know all three eigenvalues exactly at the same time. But the energy of a stationary state never depends on m in a spherically symmetric potential. All states with the same n and l but different m are degenerate.
The functions Rnl(r) depend on the exact form of the spherically symmetric potential U(r), but the functions Ylm(θ,φ) are the same for all spherically symmetric potentials. The functions Ylm(θ,φ) are called the spherical harmonics. They are the eigenfunctions of L2 and Lz, operators that do not operate on the radial coordinate r. |Ylm(θ,φ) |2 is equal to the probability density of finding the particle at angles (θ,φ). Some of the normalized spherical harmonics are given below.
![]() ,
,
![]()