Wave Equations

In the previous modules we have explored properties of mechanical wave, electromagnetic waves and matter waves.  We have studied harmonic waves and superpositions of harmonic waves, such as standing waves and wave packets.

All these waves are solution of differential equations called wave equations.  Let us write down the wave equation for a wave on a string.  The displacement of the string from its equilibrium position is denoted by y, and y is a function of position x and time t, y = y(x,t).  The function y(x,t) is a solution of the wave equation

∂2y/∂x2 - (1/v2)∂2y/∂t2 = 0,

with , where F is the tension in the string and μ = m/L is the mass per unit length of the string.

All possible waves on a string that are not driven or damped (harmonic waves, standing waves, wave pulses) satisfy this equation.  Which waves are actually realized on the string depends on the initial conditions and the boundary conditions, i.e. on how the wave is produced and what is happening on the ends of the string.

Interpreting the wave equation

The wave equation tells us how the displacement y of a string can possibly change as a function of position and time.  The key word is CHANGE.

We can look at the displacement of a string at some particular time, say t = 0.  Since the time is now fixed we can construct a plot of displacement y(x) versus position x.  Then we can find the change in y, ∆y, given a change in x, ∆x.  ∆y/∆x defines the slope of a straight line connecting the points A and B in the figure below.  As B moves closer to A, this straight line approaches the line tangent to y(x) at point A.

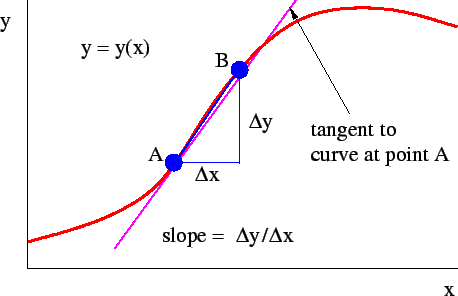The slope of this tangent line is the derivative of y with respect to x and is denoted dy/dx.  Since a tangent line to the function y(x) can be defined at any point x, the derivative itself is a function of x.  We can denote it by g(x).

g(x) = dy/dx

The slope of the tangent line at some point on the function y(x) may be approximated by the slope of a line connecting two points, A and B, set a finite distance apart on the curve.

dy/dx ~∆y/∆x

The smaller we make the distance ∆x, the better the approximation becomes.  In the limit ∆x --> 0, i.e. when the distance between A and B becomes infinitesimally small, the approximation becomes exact.

In-class activity: Exploring derivatives using a spreadsheet

Since the tangent line to the function y(x) can be defined at any point x, the derivative itself is a function of x.  The table below lists derivatives of some common functions.  In all expressions a and b are constants.

y(x) =                    

dy/dx =                    

a*xb

a*b*xb-1

a*exp(bx)

a*b*exp(bx)

a*sin(bx)

a*b*cos(bx)

a*cos(bx)

-a*b*sin(bx)

a*ln(x)

a/x

Often we will encounter functions of the form y(x) = a*exp(bx + c), y(x) = a*sin(bx + c), and y(x) = a*cos(bx + c).

The derivatives of those functions are given below.

y(x) =                    

dy/dx =                    

a*exp(bx + c)

a*b*exp(bx + c)

a*sin(bx + c)

a*b*cos(bx + c)

a*cos(bx + c)

-a*b*sin(bx + c)

Second Derivatives

The tangent line to the function y(x) can be defined at any point x, the derivative itself is a function of x which we denote it by g(x).  We can also find the slope of tangent line to the function g(x), i.e. we can find the derivative dg(x)/dx.  Taking the derivative of a derivative is called taking the second derivative.  The notation used is

 dg(x)/dx = d(dy/dx )/dx = d2y(x)/dx2.

Problems:

Find the derivatives of the following functions:
(a) y = 3x3
(b) y = 1/x
(c) y = 2√x

Find the second derivatives of the functions y = 3sin(4x).

Find the second derivatives of the function y = exp(-3x).

Partial Derivatives

Our wave function is a function of two variables, the position x and the time t.  In general, if we have a function y(x,t), the variables x and t may not be independent of each other.  Let us consider the simple function y(x,t) = x2 + t2.  If we want to take the derivative of y with respect to x while ignoring the possible dependence of t on x, we want to take a partial derivative.  We only consider the explicit dependence of the function on the differentiating variable, all other variables are taken to be constant.

A partial derivative has special notation, the "d" is replaced by "∂".  Thus, the partial derivative of y(x,t) = x2 + t2 with respect to x is ∂y/∂x = 2x, the partial derivative of y(x,t) = x2 + t2 with respect to t is ∂y/∂t = 2t.

The wave equation

So what are the solutions to our wave equation ∂2y/∂x2 - (1/v2)∂2y/∂t2 = 0?

A general solution to a second order partial differential equation like the wave equation has two arbitrary constant.  For a specific problem these constants are determined by the initial conditions and the boundary conditions.  There always exist two linearly independent solutions, i.e. the second solution is not just the first one multiplied by a constant.  Any other solution can be written as a linear combination of those solutions.

For our wave equation we have found two linearly independent solution, y = Acos(k1x - ω1t) and y = Bsin(k2x - ω2t), each with two arbitrary constants.  Any other solution is a linear combination of those solutions.  (See Wave Packets and the Fourier theorem.)

So the wave equation for waves on a string tells us that any arbitrary wave can be synthesized by a superposition of harmonic waves, as long as for those waves  |v| = ω/k = λf.