Mathematical details

In the tables below, we list the common eigenstates for the observables in each row.  The observables in each row can be measured together.  If the result of a measurement is a 1, then the system is left in a combination of the eigenstates in the left (blue) half of the cell, and if the result of a measurement is a 0, then the system is left in a combination of the eigenstates in the right (yellow) half of the cell, independent of how the initial state was prepared.

Assume we measure the observables in row 1 and obtain the results 1, 1, and 0 for the operators I * S_z, S_z * I, and -S_z * S_z respectively.  The measurement of I * S_z tells us that the system is in a combination of the eigenstates and , the measurement of S_z * I then tells us that it is in the state , and that fixes the outcome of the measurement of -S_z * S_z.

Now let us list the common eigenstates for the observables in each column.  The observables in each column can be measured together.  If the result of a measurement is a 1, then the system is left in a combination of the eigenstates in the left (blue) half of the cell, and if the result of a measurement is a 0, then the system is left in a combination of the eigenstates in the right (yellow) half of the cell, independent of how the initial state was prepared.

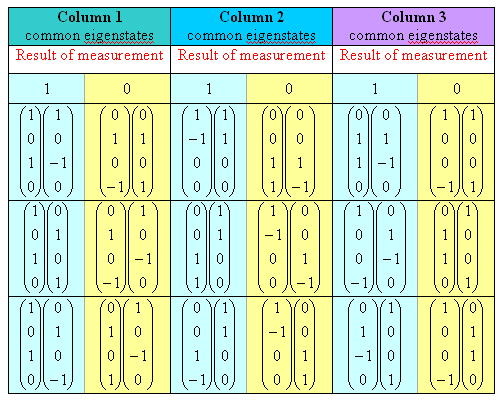
Assume we measure the observables in column 2, after having measured the observables in row 1 and having obtained the results 1, 1, and 0 for the operators I * S_z, S_z * I, and -S_z * S_z respectively.  We know that the system is in the state , which is an eigenstate of S_z * I.  This state is not listed explicitly in cell (1, 2), the top cell of column 2 in the above table, but it can be written in terms of the two state with eigenvalue 1 which are listed there, namely =   + .  It cannot be written as a linear combination of the states with eigenvalue 0.  So measuring row 1 and then measuring column 2 guaranties that we get the same result for cell (1, 2), the intersection of the row and the column.  This holds for any combination of a row (i) and a column (j).  Similarly we can show that if we first measure column 2 and then row 1, we also get the same result for cell (1, 2), the intersection of the row and the column.  It does not matter if the row or the column is measured first.