Magnetic resonance imaging (MRI) is an imaging technique used primarily in medical settings to produce high quality images of the inside of the human body.  MRI is based on the principles of nuclear magnetic resonance (NMR), a spectroscopic technique often used to obtain microscopic chemical and physical information about molecules. The medical imaging technique was called magnetic resonance imaging rather than nuclear magnetic resonance imaging (NMRI) because of the negative connotations associated with the word nuclear in the late 1970's.  MRI started out as a tomographic imaging technique (imaging by sections), that is it produced an image of the NMR signal in a thin slice through the human body.  MRI has advanced beyond a tomographic imaging technique to a volume imaging technique.

Electrons, protons, and neutrons are all spin 1/2 particles.  The spins of two such particles can combine to yield a net spin of zero.  A helium nucleus, for example, has a net spin of zero.  If a nucleus contains unpaired neutrons and protons, then it has a net spin and a net magnetic moment.  The energy of a magnetic moment of magnitude μ in a magnetic field with magnitude B pointing in the z direction is -μ_zB.  It is lowest when the magnetic moment is maximally aligned with the magnetic field and highest when the magnetic moment and the field are maximally anti-aligned.  For a net spin 1/2 nucleus only two energy states exist, separated by ∆E = 2μ_zB.  Such a magnetic moment in its low energy state can absorb a photon of energy hf = ∆E and be excited to its high energy state.  The photon frequency required is given by f = gB, g = 2μ_z/h .  For a proton, the constant g = 42.58 MHz/T.  (Tesla (T) is the SI unit for the magnetic field.)  In NMR and MRI, the quantity f is called the resonance frequency.

Some of the nuclei which are of interest in MRI are listed below.

Many magnetic resonance imagers operate at a magnetic field strength of 1.5 Tesla.  A few research units operate at 4.7 Tesla.  (For comparison, the earth magnetic field has a strength of 30 - 60 microTesla.)  What is the resonance frequency of the following nuclei in each of the magnetic fields?  ¹H,  ²³Na, ³¹P

• Solution:

  The resonant frequency is given by f = gB.

  		f (MHz)
  	g (MHz/T)	B = 1.5T	B = 4.7T
  1H	42.58	63.87	200.13
  23Na	11.27	16.91	52.97
  31P	17.25	25.88	81.08

Different chemical environments generate different local magnetic fields at the locations of the nuclei, which add vectorially to the applied field and therefore slightly shift the resonance frequency.

The energy of the two spin states can be represented by an energy level diagram.

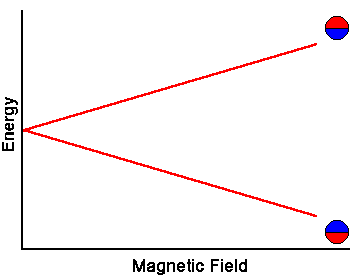
The photon energy needed to induce a transition between the two spin states is E = hf = hgB.  When the energy of a photon matches the energy difference between the two spin states, the photon can be absorbed.  In the NMR experiment, photons with frequencies in the radio frequency (RF) range are used.  In NMR spectroscopy, f lies between 60 and 800 MHz for hydrogen nuclei.  In clinical MRI, f is typically between 15 and 80 MHz for hydrogen imaging.

Problem:

What is the energy of the photon that will be absorbed by a ¹H nucleus in a 1.5 Tesla magnetic field?

• Solution:

  Given:
  B = 1.5T
  g = 42.58 MHz/T
  The energy absorbed by a ¹H nucleus is E = hf = hgB.
  E = 6.626*10^-34 Js * 42.58*10⁶ Hz/T * 1.5 T
  E = 4.23*10^-26 J

  This is a very low photon energy, when compared to the photon energy of x-rays, which are also used in medical imaging.
  For example, the energy of a f = 2*10¹⁹ Hz x-ray photon is
  E_x-ray = 6.626*10^-34 Js * 2*10¹⁹ Hz = 1.33*10^-14 J. 
  X-rays can ionize molecules and therefore damage tissue.

The simplest NMR experiment is the continuous wave experiment. There are two ways of performing this experiment.  One can hold the frequency constant and scan the magnetic field.  When the condition B = f/g is met, absorption increases.

The experiment can also be performed by holding the magnetic field constant and scanning f.  When the condition f = Bg is met, absorption increases.

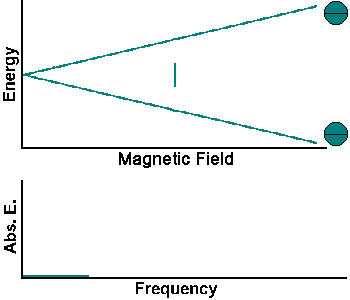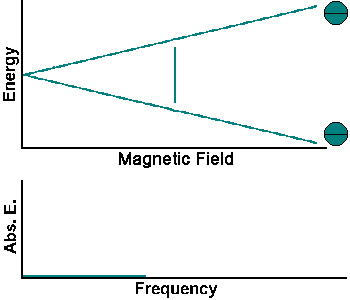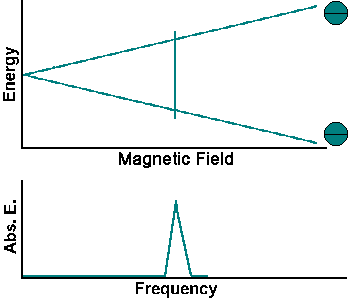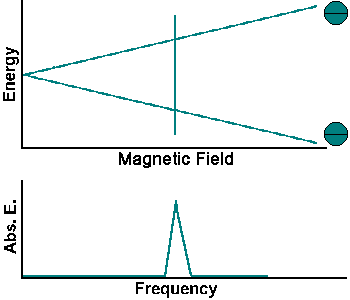
Continuous wave experiments use signal strength and frequency shift from different tissue volumes to produce contrast in an image.

Boltzmann Statistics

When a group of spins is placed in a magnetic field, the spins are either aligned or anti-aligned with the magnetic field.  At room temperature, the number of spins in the lower energy state, N⁺, slightly outnumbers the number of spins in the in the upper state, N^-.  To describe a system consisting of a large number of particles in a physically useful manner, statistical methods must be used.  Boltzmann statistics tells us that N^-/N⁺ = e^-∆E/kT.  Here k is Boltzmann's constant, 1.3805*10^-23 J/Kelvin, and T is the temperature in Kelvin.  As the temperature decreases, so does the ratio N^-/N⁺.  As the temperature increases, the ratio approaches one.

Example: 

• For ¹H nuclei in a 1.5 Tesla magnetic field ∆E = 4.23*10^-26 J.  At room temperature (~300 K) kT = 4.14*10^-21 J.  Therefore N^-/N⁺ = e^-∆E/kT = 0.9999898, very close to 1.

The signal in NMR spectroscopy is proportional to the population difference between the states.  NMR is capable of detecting very small population differences because it is a resonance technique.  To obtain a strong NMR signal one needs to work with a nuclear isotope that has a high natural abundance and for MRI  also a high biological abundance.  Protons (¹H) fulfill these requirements.  There are three isotopes of hydrogen, ¹H, ²H, and ³H.  The natural abundance of ¹H is 99.985%.  ¹H also has a high biological abundance.  The human body is primarily fat and water.  Fat and water contain hydrogen atoms.  Hydrogen nuclei have a NMR signal.  For these reasons magnetic resonance imaging primarily images the NMR signal from the hydrogen nuclei.

In-class activity: Simplified MRI

Continuous wave experiments employ one, but not the only NMR technique.  But it is cumbersome to describe non-continuous  NMR on a microscopic scale.  A macroscopic picture is more convenient.  We define a spin packet as a group of spins experiencing the same magnetic field strength.  At any instant in time, the magnetic field due to the spins in each spin packet can be represented by a magnetization vector.  (Magnetization is defined as magnetic moment per unit volume.)  The size of this vector is proportional to (N+ - N-).  The vector sum of the magnetization vectors from all of the spin packets, divided by the number of spin packets, is the net magnetization.  We assume that the coordinate system is chosen in such a way that the external magnetic field and the net magnetization vector point along the z-axis in equilibrium, when the magnitude of the net magnetization is Mz = Mo.  Mz is called the longitudinal magnetization and Mo is called the equilibrium magnetization.  One type of a pulsed NMR experiment is to change the net magnetization by exposing the nuclear spin system to RF radiation of a frequency equal to the energy difference between the spin states.  If enough energy is pumped into the system, it is possible to saturate the spin system and make Mz = 0.  The time constant which describes how Mz returns to its equilibrium value is called the spin lattice relaxation time (T1).  The equation governing this behavior as a function of the time t after the RF pulse is Mz = Mo(1 - e-t/T1).  T1 is the time to reduce the difference between the longitudinal magnetization (Mz) and its equilibrium value by a factor of e.  By monitoring the magnetization of the sample one can measure T1 and learn about the sample's environment.  Different tissues have different spin lattice relaxation times.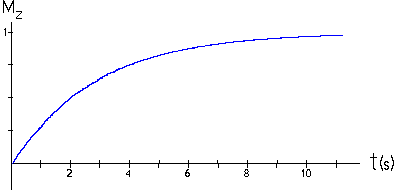

How do we monitor the magnetization?

Problem:

A sample has a T₁ of 1.0 seconds.  If the net magnetization is set equal to zero, how long will it take for the net magnetization to recover to 98% of its equilibrium value?

• Solution:

  Given: T₁ = 1.0s
  The relationship between the equilibrium net magnetization, M_o, and the net magnetization, M_z(τ), at time t is M_z = M_o(1 - e^-τ/T1).
  When M_z(τ) / M₀ = 98% we have
  0.98 = 1 - e^-τ/T1
  1 - 0.98 = e^-τ/T1
  ln( 0.02 ) = -τ/T₁
  -T₁ * ln( 0.02 ) = τ
  -1.0 s * ln( 0.02 ) = 3.9 s = τ

Longitudinal spin relaxation is just one of several non-continuous NMR techniques probing the environment of the sample.  Nuclear magnetic relaxation times of tissues and tumors are differed, which motivates the use of  magnetic resonance techniques for the detection of disease.

Link:  The Basics of MRI