

Elementary particles have intrinsic properties. Some of these properties are the same properties we associate with macroscopic objects, such as mass and charge. Some are purely quantum-mechanical and have no macroscopic analog.
Spin is intrinsic angular momentum associated with elementary particles. It is a purely quantum mechanical phenomenon without any analog in classical physics. Spin is not associated with any rotating internal parts of elementary particles; it is intrinsic to the particle itself. An electron has spin, even though it is believed to be a point particle, possessing no internal structure. The concept of spin was introduced in 1925 by Ralph Kronig, and independently by George Uhlenbeck and Samuel Goudsmit.
Spin is quantized, and can only take on discrete values. The spin angular momentum of an electron, measured along any particular direction, can only take on the values ħ/2 or -ħ/2. We denote the spin of a particle by S and its component along the z-axis by Sz. The eigenvalues of the square of the magnitude of the spin operator are S2 = s(s+1)ħ2, and the eigenvalues of the Sz operator are msħ, where ms can take on values from -s to +s in integer steps. For the electron s = 1/2 and S2 = (3/4)ħ2.
 |
We can measure the orientation of the electron spin with respect to any axis (spin polarization). These measurements yield two possible values,~55o aligned or anti-aligned. Measurements of the orientation with respect to the x-, y-, and z-axis are incompatible.
|
For all particles spin quantum number s is restricted to integer or half-integer values. Elementary particles for which s = 1/2, 3/2, ..., are called fermions and elementary particles for which s = 0, 1, 2, ..., are called bosons. Electrons, protons, and neutrons are all spin 1/2 particles. Photons are spin 1 particles, and certain exotic particles, such as pions, possess spin zero.
Most particles with spin possess a magnetic moment. This magnetic moment can be experimentally observed, by passing the particles through an inhomogeneous magnetic field in a Stern-Gerlach type experiment, or by measuring the magnetic fields generated by the particles themselves. Ferromagnetism arises from the alignment of the spins of the atomic electrons in a solid.
The magnetic moment μ arising from the spin of the electron is proportional to S, μ = γS, with γ = -|qe|/me a constant of proportionality. The proportional constant γ for spin has twice the magnitude of the proportional constant γ for orbital angular momentum. Since Sz is quantized, μz is quantized, μz = -|qe|msħ/me. For an electron ms = 1/2 or -1/2, and the possible values of μz are μB and -μB. Here μB = |qe|ħ/(2me) is the Bohr magneton.
Assume an "electron gun" produces a beam of electrons. (The electrons should be in a system that has no net charge and zero orbital angular momentum. A ground-state hydrogen atom is an example of such system.) Assume the electrons are moving into the y-direction and pass through a magnet with an inhomogeneous field pointing into the negative z-direction. In the figure below the magnetic field points from the north pole to the south pole. The magnitude of the field is larger near the north pole, because of the taper of the north pole piece. The force experienced by a magnetic moment is Fz = μzdBz/dz. Here dB/dz is negative, since B becomes more negative as z increases. For a particle with Sz = ħ/2, the z-component of the magnetic moment, μz, is negative, and therefore Fz is positive. A particle with Sz = ħ/2 is deflected upward. A particle with Sz = -ħ/2 is deflected downward. The amount of deflection up or down is exactly the same.

Since the spins of the electrons from the electron gun are randomly oriented, 50% of the electrons in the beam are deflected upward and the other 50% are deflected downward. Before the magnet we cannot predict whether an individual electron will be deflected upward or downward. But after an electron has passed through the magnet, we know the z-component of its spin. We have constructed a spin analyzer.
Now consider an arrangement of three magnets in series with the polarity of the middle, longer magnet reversed. The paths of spin-up or spin-down electrons through the arrangement are different, but both spin orientations emerge undeflected. If we insert a beam block, only spin-up particles can pass.
 |
 |
 |
With the beam block in place, one half of the incident electrons will be stopped inside the apparatus, while the other half will emerge undeflected. We have constructed a spin filter for spin-up electrons.
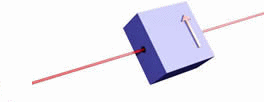
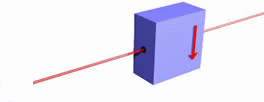
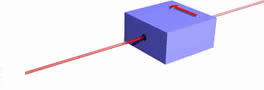
Let us schematically represent the spin filter by a box as shown in the figure below. The arrow on the front side of the box indicates what direction is "up." Only spin-up electrons can pass.

If we change the orientation of the box, we always observe that 50% of the incident electrons from the gun emerge from the filter box, while the other 50% do not, independent of the orientation. For all the orientations shown below 50% of the incident electrons emerge, while the other 50% do not.
 |
 |
 |
Now let us put two filters in series. If we put a second filter behind the first filter with the same orientation as the first filter, then the second filter has no effect. 50% of the electrons from the electron gun emerge from the first filter, and all of those electrons pass through the second filter. Once we have measured that an electron is in the eigenstate of Sz with eigenvalue ħ/2, a second measurement will yield the same result.
If we reverse the orientation of the second filter, then the second filter will stop all electrons. 50% of the electrons from the electron gun emerge from the first filter, and none of those electrons will pass through the second filter. The first filters definition of "up" is the second filters definition of "down".
Now let us orient the second filter at 90° relative to
the first one. Once again, 50% of the electrons from the
electron gun emerge from the first filter. 50% of those
electrons will pass through the second filter. So if we have two
definitions of "up" from two filters at right angles to each other,
50% of the electrons that satisfied the first definition will then satisfy
the second definitions
If we slowly rotate the orientation of the second filter with respect to
the first one from zero degrees to 180 degrees, the fraction of the
electrons emerging from the first filter which will pass the second
filter changes continuously from 100% to 0%.
If the relative angle is θ, the percentage of
electrons passing the second filter after having passed the first filter is 100% * cos2(θ/2).
Photons are spin 1 particles. The spin of a photon is measured by making polarization measurement. If we measure the linear polarization of a single photon along any axis, we can only find it aligned with the axis or perpendicular to this axis. If we measure the linear polarization of photons along any axis, there are only two possible results. To measure the polarization we can use a polaroid filter. It has a transmission axis and only passes photons whose polarization is aligned with this axis. Photons whose polarization is perpendicular to the transmission axis are stopped. The polaroid filter becomes a "spin filter".
Assume we use a polaroid filter. One half of the photons from an incandescent lamp will pass through such a filter. If a second filter is placed behind the first one and the axes of both filters have the same orientations, all the photons will pass the second filter (at least in the case of perfect polaroid filters). If the relative orientation of the axes of the two polaroid filters is 90°, then no light will emerges from the second filter. If the relative orientation of the axes of the two polaroid filters is 45°, one half of the photons that pass the first filter will also emerge from the second filter. The only difference between the actions of two electron spin filters and two polaroid filters for light is a factor of 2 in the relative orientations.
Below we consider one final combination of electron filters.
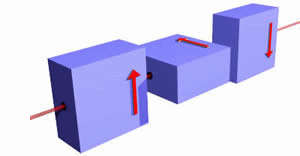
One-half of the beam of electron from the gun emerges from the first filter. 50% of those electrons emerge from the second filter. And 50% of those electrons will make it through the third upside-down filter. Note that if the second filter is not present, no electrons emerge from the upside-down filter.
In class activity: A Stern-Gerlach experiment
We denote the eigenstates of the Sz operator by |+> and |->. The Sz operator is associated with a measurement of the z-component of the spin. For an electron, this measurement can have two outcomes.
Sz|+> = ħ/2|+>, Sz |-> = -ħ/2|->.
We denote the eigenstates of the Su operator by |+>u and |->u. The Su operator is associated with a measurement of the component of the spin along an axis u defined by two angles (θ, φ)u. For an electron, this measurement can have two outcomes.
Su|+>u = ħ/2|+>u, Su |->u = -ħ/2|->u.
Sz and Su are incompatible observables. The eigenstates of the operator Su associated with measuring the projections of the spin along an axis defined by the angles (θ, φ)u are linear combinations of |+> and |-> .
|+>u = a|+> + b |->, |->u = c|+> + d |->.
After a measurement of Su, the particle is in an eigenstate of Su. Assume we have measured Su = ħ/2. Then the particle is in the eigenstate |+>u = a|+> + b |->. Assume now we perform a second measurement and measure Sz. The probability that we will measure ħ/2 is |a|2 and the probability that we will measure -ħ/2 is |b|2.
If we measured Su = -ħ/2 then the particle is in the eigenstate |->u = c|+> + d |->. Assume now we perform a second measurement and measure Sz. The probability that we will measure ħ/2 is |c|2 and the probability that we will measure -ħ/2 is |d|2.
For normalized states we have |a|2 + |b|2 = 1, |c|2 + |d|2 = 1.
The coefficients a, b, c, and d are given below.
![]() .
.
For the x-directions we have θ =
π/2, φ = 0.
The eigenvectors of Sx therefore can be written as |+>x
= 2-1/2(|+>
+ |->) and |->x = 2-1/2(|+> - |->).
Overall multiplicative factors of magnitude one cause no observable
effect and can be omitted.
For the y-directions we have θ =
π/2, φ = π/2.
The eigenvectors of Sy therefore can be written as |+>y
= 2-1/2(|+>
+ i|->) and |->y = 2-1/2(|+> - i|->).
We can only know the components of the spin along one axis at any one time. If we measure the component along a second axis, we lose the information about the component along the first axis
Assume we have measured Su(θ, φ) = ħ/2, and we now perform a second measurement and measure Sz. The probability that we will measure ħ/2 is cos2(θ/2), and the probability that we will measure -ħ/2 is sin2(θ/2).
Problem:
The figure below shows a sequence of measurements.
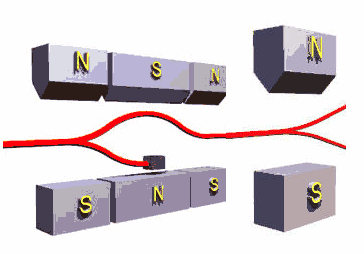
What percentage of electrons from an electron gun will leave the spin analyzer in the spin up state?
Solution:
50% of the electrons from the gun will pass the spin filter. They will be in the spin up state. They all will leave the analyzer in the spin up state. So 50% of the electrons from the gun will leave the analyzer in the spin up state.