In-class group activity 14:
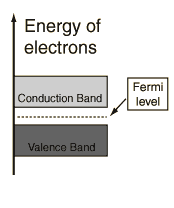
Semiconductors have a small gap between the valence and the conduction band. At room temperature some electrons can gain enough energy from thermal agitation to lift them from the valence band to the conduction band.
Quantum Dots are small semiconductor particles with a radius of a few nanometers. The Quantum Dots in our solutions are made from indium phosphide. The band gap for this semiconductor in bulk is
Eg = 2.15*10-19 J.
Photons with energy hf > 2.15*10-19 J = 1.34 eV can excite electrons from the valence into the conduction band in bulk material.
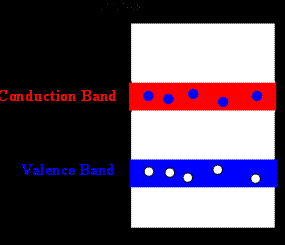
In the conduction band the electrons are free to move and can be modeled as a free particle in a box with effective mass
me(eff) = 7.29*10-32 kg.
The holes in the valence band are also free to move and can be modeled as a free particle in a box with effective mass
mh(eff) = 5.47*10-31 kg.
The ground state energy of a particles in a 3D spherical box is E = π2ħ2/(2mR2). For large boxes (large Quantum Dots, R > mm) the ground state energy is practically zero. But for small boxes (small Quantum Dots) this ground state energy can be comparable to the band gap Eg, and a photons needs appreciably more energy to excite and electron from the valence to the conduction band than in bulk material.
Ephoton = π2ħ2/(2me(eff)R2) + π2ħ2/(2mh(eff)R2) + Eg.
[Creating the electron hole pair takes energy Eg. But in a small box the electron and the hole cannot be created with zero energy. The minimum energy the electron must receive is its ground state energy in the box, π2ħ2/(2me(eff)R2), and the minimum energy the hole must receive is its ground state energy in the box, π2ħ2/(2mh(eff)R2).
When the electron and the hole recombine, a photon is emitted. By measuring the energy of the photons that are emitted, we can determine the size of the Quantum Dots.
R2 = 0.5*π2ħ2(1/me(eff) + 1/mh(eff))/(Ephoton
- Eg)
= [8.52*10-37/(1.99*10-25/λ(m)
- 2.15*10-19)]m2.
Task:
For four different samples of Quantum Dots excite the dots using a 380 nm LED. Measure the wavelength λ of the photons emitted by the dots when the electrons and holes recombine with the Ocean Optics Red Tide Spectrometer and calculate R. Enter your results into a table.
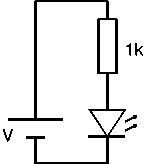
LED circuit diagram