

Superconducting materials in their superconducting state have no resistance. They are in this state at temperatures below a critical temperature Tc. In addition superconducting materials either expel magnetic fields completely or confine them to filaments when they are in the superconducting state. Superconductivity is of technological importance. For example, the large magnets used in medical resonance imaging are wound with superconducting wires. The currents necessary to produce the strong magnetic fields would produce too much thermal energy in ordinary wires.
We can understand the basic physical principles that lie behind the phenomenon of conventional superconductivity. When discussing fermions and the Fermi energy in metals, we ignored all dynamic interactions among the electrons. How can this make sense, given that electrons repel each other because of their electric charges? The exclusion principle explains why electron-electron interactions are not very important in ordinary metals. Consider two electrons in different states. Their interaction would manifest itself in some change of state. However, the vast majority of electrons cannot change states because the states above and below their own state are already fully occupied, and the exclusion principle forbids further occupation. Interactions do lead to some modification of the predictions of the free-electron theory, but these modifications are well understood.
The phenomenon of superconductivity also involves interactions, but this time between the electrons and the vibrating lattices of ions in a metal. For complicated reasons that were first understood by Leon Cooper, the electron-ion interaction has as a secondary effect a weak attraction between electrons with energies that are close to the Fermi energy. This attraction leads to the formation of weakly bound pairs of electrons known as Cooper pairs. Their binding is so weak that they can be quite far apart from each other, as much as hundreds of lattice spacings. This means that the wave function of the bound state is very spread out. Indeed, this is the only way the pair can exist in the presence of a Coulomb repulsion. The Coulomb force between the electrons is screened by the presence of the lattice when the electrons are far apart. The spread-out wave function means that many Cooper pairs may overlap each other. Although different pairs overlap spatially, the two electrons that make up a Cooper pair are tightly related, acting as a true pair. The electrons have equal and opposite momenta, and opposite spins. The pairs have lower energies than free electrons. It takes some energy to separate the electrons that form a pair. An energy gap of width 2∆ ~10-3 eV develops about the Fermi energy, meaning that there are no electron states with energies that lie between EF - ∆ and EF + ∆. The gap width is small compared to the Fermi energy itself.
John Bardeen, Leon Cooper, and Robert Schrieffer constructed a theory in 1957, the BCS theory, that explained satisfactorily all of the observations about superconductors known at the time. For most superconducting materials a Cooper pair has a total angular momentum of 0. Although, strictly speaking, a pair cannot be treated as a boson such as a helium atom, a pair shares some crucial properties with bosons. In particular, the BCS theory predicts that the Cooper pairs all condense into the same state when the temperature drops below a critical temperature Tc. Tc is approximately given by the gap width divided by the Boltzmann constant. This condensation signals an abrupt change in the properties of the metal, a change somewhat analogous to the phase change from liquid to solid.
The most striking property of superconductors is that they have no resistance below Tc. This phenomenon is explained by the coherence of the superconducting state. Many Cooper pairs are in their lowest energy state. A large number of electron pairs move together in a coordinated way. For the superconductor to lose energy, the entire coherent state would have to be broken up, and this would require a large amount of energy to be supplied at once.
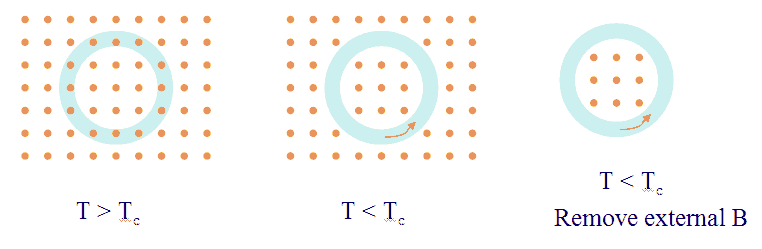
The Meissner effect is another striking property of superconductors. No magnetic field can penetrate a superconductor and a magnetic field already present is expelled when a metal is cooled below Tc. If you try to increase a magnetic field inside a superconductor, you will induce an electric field within the material according to Faraday's law. Lentzís rule states that a current will flow to oppose the change that produced it. Because all the Cooper pairs act together, even the tiniest change in magnetic flux can generate a current which flows without resistance and and produces its own magnetic field, which cancels entirely the inducing field within the superconductor.
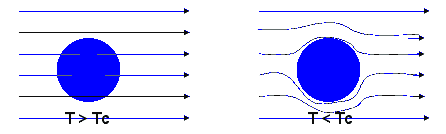
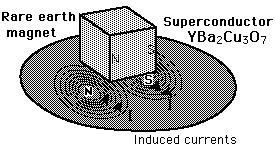
If a small magnet is brought near a superconductor, it will be repelled because induced super-currents will produce mirror images of each pole. If a small permanent magnet is placed above a superconductor, it can be levitated by this repulsive force.

Link: The Meissner effect
Flux Quantization
Suppose that we place into a magnetic field a ring of superconducting material that is above its critical temperature. The ring lies in a plane perpendicular to the field direction. We now lower the temperature of the material below Tc, so that the material becomes superconducting. The field is expelled, and all the field lines will be either outside the ring or confined within the ring. The BCS theory can be used to show that the coherence of the superconducting state implies that the magnetic flux through the ring is quantized in units of Φ0 = h/2e:
The quantity Φ0 is the magnetic flux quantum, with value 2.07 *10-15 Tm2. The charge 2e that appears here is the charge of a Cooper pair. The prediction that flux is quantized has been successfully tested by experiment.
In conventional superconductors, superconductivity is caused by a force of attraction between certain conduction electrons, which causes them to act as correlated pairs. There also exists a class of materials, known as unconventional superconductors, that exhibit superconductivity, but whose physical properties contradict the theory of conventional superconductors. In particular, the so-called high-temperature superconductors superconduct at temperatures much higher than should be possible according to the conventional theory. There is currently no complete theory of high-temperature superconductivity.
Superconductivity occurs in a wide variety of materials, including simple elements like tin and aluminum, various metallic alloys, some heavily-doped semiconductors, and certain ceramic compounds containing planes of copper and oxygen atoms. The latter class of compounds, known as the cuprates, are high-temperature superconductors. Superconductivity does not occur in noble metals like gold and silver, nor in ferromagnetic metals.
Link: