Nuclear Properties

At the end of 1895, Wilhelm Roentgen discovered X-rays and in 1896 Becquerel, experimenting with Uranium, discovered radioactivity.   In 1897 J. J. Thomson discovered the electron, a negatively charged particle more than two thousand times lighter than a hydrogen atom.  In 1906 Thomson suggested that each atom contained a number of electrons roughly equal to its atomic number.  Since atoms are neutral, the charge of these electrons must be balanced by some kind of positive charge.  Thomson proposed a 'plum pudding' model, with positive and negative charge filling a sphere only one ten billionth of a meter across.  This plum pudding model was generally accepted.  Even Thomson's student Rutherford, who would later prove the model incorrect, believed in it at the time

While studying in the Cavendish, Ernest Rutherford became fascinated by radioactivity.  He investigated it for twenty years. Rutherford confirmed Becquerel's observation that there were at least two parts to the uranium rays.  Rutherford named the easily absorbed rays "alpha" and the more penetrating rays "beta".  He went on to discover that these rays were particles.

Rutherford measured the specific charge of the alpha particles by deflecting them in electric and magnetic fields.  Rutherford measured the deflection of the alpha particles by measuring their position on a photographic film.  While making the measurements, he observed an unusual effect.  If the alpha particles passed through a thin sheet of mica, the images on the film were blurred.  The images were sharp if the mica was not present.  Something about the mica sheet was causing the alpha particles to scatter at seemingly random small angles, resulting in the blurred images.  Rutherford continued to investigate scattering of alpha particles, and working with Geiger and Marsden, a graduate student of Geiger, Rutherford suggested that Marsden look for alpha-particle scattering at large angles, even though he did not think it was very likely that it occurred.

Geiger and Marsden scattered ~5.5 MeV alpha particles off a gold foil and observed some particles scattering through very large angles, some even appearing to bounce right back at the source of the particles.  Rutherford described it as the most incredible event of his life, "as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you."  Such huge deflections could not be explained by Thomson's model of the atom, where charge was distributed evenly throughout the atom.  For such large deflections all the positive charge had to be concentrated in a small mass greater than the mass of the alpha particles.  The force that could cause such large deflections had to be large.  The positively charged alpha particles were being repelled by a massive positively charged object.  The positive charge in an atom of gold was known, but if this charge were collected on a sphere the size of the atom, the repulsion would be far too weak. To explain the force experienced by the alpha particle the charge would have to be collected in a much smaller sphere.

In 1911 Rutherford proposed that each atom has a massive nucleus containing all of its positive charge, and that the much lighter electrons are outside this nucleus.  The nucleus has a radius about ten thousand times smaller than the radius of the atom, only ten femtometers.  Scattering at large angles occurs when the alpha particles come close to a nucleus.  The reason that most alpha particles are not scattered at all is that they are passing through the relatively large 'gaps' between nuclei.

Rutherford revised Thomson's 'plum pudding' model, showing how electrons could orbit a positively charged nucleus, like planets orbiting a star.  In 1915 Niels Bohr adapted Rutherford's model by saying that the orbits of the electrons were quantized, meaning that they could exist only at certain distances from the nucleus.

Simulation: Rutherford Scattering

Link:

The Rutherford scattering experiment worked because the size of the wave packet of a 5.5 MeV alpha particle is on the order of the size of the nucleus.  The deBroglie wavelength of a 5.5 MeV alpha particle is λ = h/(2mE)1/2 = 6.4*10-15 m.  So the alpha particle can be used to find the nucleus inside the atom.  To look for structure within a nucleon, one needs particles whose deBroglie wavelength is much less than 10-15 m.  In the late 1960s, deep inelastic scattering experiments with up to 20 GeV electrons showed that even protons have internal subcomponent structure.

Ernest Rutherford discovered that all the positive charge of an atom was located in a tiny dense object at the center of the atom.  By the 1930s, it was known that this object was a ball of positively charged protons and electrically neutral neutrons packed closely together.  Protons and neutrons are called nucleons.  The nucleus is a quantum object.  We cannot understand its properties and behaviors using classical physics.  We cannot track the individual protons and neutrons inside a nucleus.  Nevertheless, experiments have shown that the "volume" of the nucleus is proportional to the number of nucleons that make up the nucleus.  We define the volume of the nucleus (and also the volume of any other quantum particle) as the volume of the region over which its interaction with the outside world differs from that of a point particle, i.e. a particle with no size.

With the above definition of the volume and size of a quantum particle we find that protons and neutrons are each about 1.4*10–15 m in diameter, and the size of a nucleus is essentially the size of a ball of these particles.  For example, iron 56, with its 26 protons and 30 neutrons, has a diameter of about 4 proton diameters.  Uranium 235 is just over 6 proton diameters across.  One can check, for example, that a bag containing 235 similar marbles is about six marble diameters across.

Most nuclei are approximately spherical.  The average radius of a nucleus with A nucleons is R = R0A1/3,  where R0 = 1.2*10-15 m.  (Think about: How can we define and measure the radius of a nucleus?)  The volume of the nucleus is directly proportional to the total number of nucleons.  This suggests that all nuclei have nearly the same density.  Nucleons combine to form a nucleus as though they were tightly packed spheres.

Problem:

What is the density of nuclear matter?

That the nucleus exists means that there is some force other than the electrostatic force or gravity which holds it together.  The protons are all repelling each other electrically, the neutrons are electrically neutral, and the attractive gravitational force between protons is some 10–38 times weaker than the electrostatic repulsive force.  The force that holds the nucleus together must be attractive and even stronger than the electrostatic repulsion.  This attractive force is called the nuclear force.  The nuclear force treats protons and neutrons equally, it does not differentiate between a proton and a neutron.  The nuclear force is charge independent.  For this reason we talk about the nuclear force between nucleons.  The nuclear force does not act on electrons.  The properties of the nuclear force can be deduced from the properties of the structures it creates, namely the atomic nuclei.  The fact that protons and neutrons maintain their size while inside a nucleus means that the nuclear force is both attractive and repulsive.  If we try to pull two nucleons apart, the attractive nuclear force holds them together, next to each other.  But if we try to squeeze two nucleons into each other, we encounter a very strong repulsion, giving the nucleons essentially a solid core.  It is the repulsive part of the nuclear force that makes nuclear matter nearly incompressible.

While the attractive nuclear force must be stronger than the electrostatic force to hold the protons together in the nucleus, it is not a long range 1/r2 force like the electrostatic force and gravity.  It drops off much more rapidly than 1/r2, with the result that if two protons are separated by more than a few proton diameters, the electric repulsion becomes stronger than the nuclear attraction.  The separation D0 at which the electric repulsion becomes stronger than the nuclear attraction is about 4 proton diameters.  This distance D0, which we will call the range of the nuclear force, can be determined by looking at the stability of atomic nuclei.  If we start with a small nucleus, and keep adding nucleons, for a while the nucleus becomes more stable if we add the right mix of protons and neutrons.  By more stable, we mean more tightly bound.  The more stable a nucleus is, the more energy is required, per nucleon, to pull the nucleus apart.  This stability is caused by the attractive nuclear force between nucleons.

Iron 56 is the most stable nucleus.  It takes more energy per nucleon to take an Iron 56 nucleus apart than any other nucleus.  If the nucleus gets bigger than Iron 56, it becomes less stable, less tightly bound.  If a nucleus gets too big, bigger than a Lead 208 or Bismuth 209 nucleus, it becomes unstable and decays by itself.  The stability of Iron 56 results from the fact that an Iron 56 nucleus has a diameter about equal to the range of the nuclear force.  In an Iron 56 nucleus every nucleon is attracting every other nucleon.  If we go to a nucleus larger than Iron 56, then neighboring nucleons still attract each other, but protons on opposite sides of the nucleus now only repel each other.  This repulsion between distant protons leads to less binding energy per particle and instability.  (We usually give the binding energy of a nucleus as a positive number.  It then is the energy that is needed from an external source to separate the nucleus into its constituent protons and neutrons.)

Link:  Dense packing of spheres

The simplest nucleus, that of hydrogen, is a single proton.  The proton is an elementary particle of mass about 940 MeV, positive charge exactly opposite to the electron’s charge, and spin one-half.  It is a fermion.  (Note: we are giving mass here in units of energy, we are giving mc2.)  No two protons can be in exactly the same quantum state.  The next simplest nucleus is the deuteron.  It is a bound state of a proton and a neutron.  The neutron, like the proton, is a spin one-half fermion, but it has no electric charge, and is slightly more massive than the proton.  The binding energy of the deuteron is 2.2 MeV.  A photon of this energy could "ionize" the deuteron into a separated proton and neutron.  However, it is not necessary to actually do this experiment to establish how tightly the deuteron is bound.  One only needs to weigh the deuteron accurately.  It has a mass of 1875.61 MeV.  The proton has a mass of 938.27 MeV, the neutron 939.56 MeV, so the sum of their masses is 1877.83 MeV, 2.2 MeV more than the deuteron mass.  Thus, when a proton and a neutron come together to form a deuteron, they must release 2.2 MeV of energy, which they do by emitting a γ ray.  The total number of nucleons in a nucleus is usually denoted by the mass number A, where A = Z + N, Z protons and N neutrons.  The chemical properties of an atom are determined by the number of electrons, the same as the number of protons Z.  This is called the atomic number.  Nuclei can have the same atomic number, but different numbers of neutrons.  These nuclei are called isotopes, the Greek for "same place", since they are in the same place in the periodic table. 

Chart of Nuclides


Physicists map the inventory of known nuclei on a "chart of nuclides."  On the chart shown above, the vertical axis represents the number of neutrons a nucleus contains and the horizontal axis represents the number of protons it possesses.  The region of stable nuclei is roughly found on a diagonal line, where the neutron number approximately equals proton number.  Above this diagonal is a jagged line called the "neutron dripline" and below this diagonal is another jagged line called the "proton dripline."  Nuclei found below the proton dripline and above the neutron dripline tend to be highly unstable and undergo radioactive decay readily.

Link:

The best way to see the competition between the attractive nuclear force and the electric repulsive force inside atomic nuclei is to look at nuclear binding energies.  The binding energy per nucleon (proton or neutron) represents how much energy we would have to supply to pull the nucleus apart into separate free nucleons.  The nuclear force tries to hold the nucleus together, and therefore increases the binding energy.  The electrostatic force, which pushes the protons apart, decreases the binding energy.  We calculate the binding energy of a nucleus by subtracting the rest energy of the nucleus from the sum of the rest energies of the protons and neutrons that make up the nucleus.  We then divide by the number of nucleons to get the binding energy per nucleon.   For the deuteron the binding energy per nucleon is therefore 1.1 MeV.

Problem:

Given the mass of the alpha particle, mc2 = 3727.38 MeV,  find  the binding energy per nucleon.

We use the following notation to describe a nucleus:

AZX, where X is the chemical symbol of the element 

Example:

2713Al
 

 

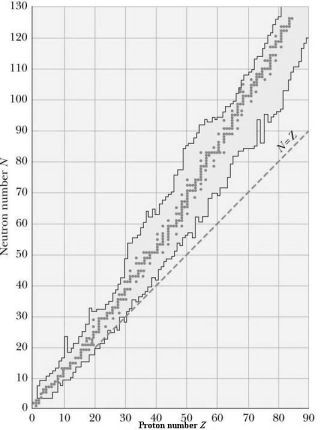
The figure above is a plot of the binding energy, per nucleon, of the most stable nuclei for each element.  The peak of that curve is at the Iron 56 nucleus, no other nucleus is more tightly bound.  Except for light nuclei, the binding energy is about 8 MeV per nucleon.

Moving towards higher binding energy represents a release of energy.  There are two ways to do this.  We can start with light nuclei and put them together to form heavier nuclei, moving in and up from the left side in the figure.  This process is called nuclear fusion.  Or we can split apart heavy nuclei moving in and up from the right side.  This process is called  nuclear fission.  Fusion represents the release of nuclear potential energy, while fission represents the release of electric potential energy.  When we get to Iron 56, there is no energy to be released either by fusion or fission.

The reason Iron 56 is most strongly bound is because the diameter of an iron nucleus is about equal to the range of the nuclear force.  At Iron 56, you have the largest nucleus in which every particle attracts every other particle.  The diameter of the Iron 56 nucleus is the distance over which the attractive nuclear force is stronger than the repulsive electrostatic force.  There are some bumps in the graph of nuclear binding energies, bumps representing details in the structure of the nuclear force.  The most striking anomaly is the Helium 4 nucleus which is far more tightly bound than neighboring nuclei.  This tight binding of Helium 4 is the reason that α particles rather than individual protons are emitted in radioactive decays.

The importance of knowing the nuclear binding energy per nucleon is that it tells us whether energy will be released in a particular nuclear reaction.  If the somewhat weakly bound uranium nucleus (7.41 MeV/ nucleon) splits into two more tightly bound nuclei like cesium (8.16 MeV/nucleon) and zirconium (8.41 MeV/ nucleon), energy is released.  At the other end of the graph, if we combine two weakly bound deuterium nuclei (2.8 MeV/nucleon) to form a more tightly bound Helium 4 nucleus (7.1 MeV/nucleon), energy is also released.  Any reaction that moves us toward the Iron 56 nucleus releases energy.

Binding energy formula

Atomic and nuclear data tables often list the mass of the neutral atom (not that of the nucleus) in atomic mass units (u).  One u is 1/12th of the mass of the neutral carbon atom, 1 u = (1/12)m12C.  This can easily be converted to SI units.  One mole of 12C weighs 0.012 kg, and contains Avogadro's number particles, thus 

1 u = 0.001kg/NA = 1.66054*10-27 kg = 931.494 MeV/c2.

We can write down a formula for the binding energy of a nucleus in terms of the nuclear masses or in terms of the atomic masses.  The binding energy is defined as the the total mass energy of constituent nucleons minus the mass energy of the nucleus.  It is the total energy one needs to invest to decompose the nucleus into nucleons.

In terms of the nuclear masses, we write for the binding energy B(Z,N) of a nucleus with Z protons and N neutrons

B(Z,N) = c2(Z*mp + N*mn - Mnuc(Z,N)).

In terms of the atomic masses, we write

B(Z,N) = c2(Z*mH + N*mn - Matom(Z,N)).

The masses of the Z electrons cancel out and the difference in binding energies of the electrons in the different atoms (~eV) is negligible compared to the nuclear binding energy (~MeV).

Problems:

What is the binding energy per nucleon for 120Sn?

What is the binding energy per nucleon for 262Bh?  The mass of the atom is 262.1231 u.

The binding energy per nucleon of 239Pu (Z = 94) is 7.56 MeV.  Find the mass of the Plutonium nucleus and the mass of the neutral atom in atomic mass units.