
A given spring is "lousy" in the sense that it loses its elastic properties over time. To describe this, let the restoring force of the spring be expressed as F(x) = -k(x - x0)e-t/τ, where k and τ are constants, x is the position of the mass m attached to the spring, and x0 is the position of equilibrium.
(a) Does the potential energy exist? If so, find it. If not, motivate your
answer.
(b) Is mechanical energy conserved? If so, prove it. If not, determine the
amount of energy lost per unit time.
Two small metallic spheres are suspended from a common point as pendulums by light strings of length 0.3 m. The mass of each sphere is 0.2 g. They are given the same electric charge. They come to equilibrium when each string is at an angle of 5 degrees to the vertical. What is the magnitude of the charge on each sphere?

Two identical billiard balls of radius R and mass M, rolling with CM velocities
±vi, collide elastically, head-on.
Assume that after the collision they have both reversed motion and are
still rolling.
(a) Find the
impulse which the surface of the table must exert on each ball during its
reversal of motion.
(b) What
impulse is exerted by one ball on the other?
Consider the ring of mass M shown in the figure. Assume that the ring is thin and has a uniform density. A particle of mass m is placed a distance x from the center of the ring, on a line that passes through the center of the ring and is perpendicular to its plane.
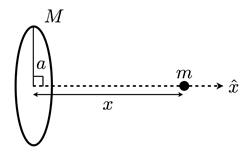
(a)
Calculate the gravitational potential energy of this system, assuming that the
potential is zero at infinity.
(b)
Calculate the gravitational force acting on the particle.
(c)
Derive expressions for gravitational potential energy and force in the limit
x >> a.
(d)
Why would you expect the result in (c)?