∫ x sin(x)dx = sin(x) - x cos(x)
∑n=0, odd∞1/n2 = π2/8
Consider a particle with mass m and energy E traveling in one-dimension from x = -∞. Calculate the probability for it to tunnel, i.e. the transmittance T, through a square potential barrier of height U0 > E located at 0 ≤ x ≤ L.
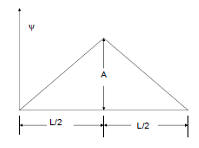
A particle moving in one dimension is confined to an
infinite square well of width L. At t = 0 its wave function is piecewise
linear and symmetric about L/2 with a maximum height of A, as shown.
(a)
Normalize the wave function and find A.
(b)
Write down the normalized eigenfunctions in this potential.
(c) Expand ψ(0)
in terms of the eigenfunctions of part (b).
(d) Write an expression for ψ(x,t).
How much time T must elapse in order for ψ(x,T) = ψ(x,0)?
(e)
rite down an expression for <E>, the expectation value of the particles energy in this state.

∫ x sin(x)dx = sin(x) - x cos(x)
∑n=0, odd∞1/n2 = π2/8
A system has a wave function ψ(x,y,z) = N*(x + y + z)*exp(-r2/α2) with α real. If Lz and L2 are measured, what are the probabilities of finding 0 and 2ħ2?
An electron is a rest in magnetic field B = B0 k + B1(cos(ωt)
i + sin(ωt) j). B0, B1, and ω are
constants. At t = 0 the electron is in the |+> eigenstate of Sz.
Let μ = -γS be the magnetic moment of the electron and ω0
= γB0, ω1 = γB1 be constants.
(a)
Construct the Hamiltonian matrix for this system and write down the
time-dependent Schroedinger equation,
iħ
| ∂α/∂t | ||
| ∂β/∂t |
= H(t)
| α | ||
| β |
.
in matrix form in the {|+>, |->} basis.
(b) Convert this equation into a "Schroedinger equation"
with a time independent "Hamiltonian"
by choosing new expansion coefficients
a(t) = exp(iωt/2)α(t), b(t) = exp(-iωt/2)β(t).
(Hint: Given
∂α/∂t and ∂β/∂t
find ∂a/∂t and ∂b/∂t.)
(c) Find the eigenvalues and
eigenvectors if the "Hamiltonian" in part (b).
Hint: Write
H' = A
| cosθ | sinθ | ||
| sinθ | -cosθ |
.
The eigenvalues of the matrix are λ = ±1, and the
corresponding eigenvectors are
|ψ+> = cos(θ/2)|+> +
sin(θ/2)|->, |ψ->
= -sin(θ/2)|+> + cos(θ/2)|->.]
(d)
The Schroedinger equation now implies that
U(t,0)|ψ+>
= |ψ+>exp(-iAλ+t/ħ),
and U(t,0)|ψ-> = |ψ->exp(-iAλ-t/ħ).
Find the
probability of finding the electron in the |-> eigenstate of Sz as a
function of time.