Problem 1:

A particle of mass m moves in a central potential U(r) = kr²e^-r/a, with k and a positive constants.
(a)  Write down the Lagrangian for this system and determine the second-order equations of motion in polar coordinates. 
(b)  For what values of b is a circular orbit of radius b possible?
(c)  For a circular orbit of radius a, write down the angular momentum M in terms of m, k and a.
(d)  Is a circular orbit of radius a a stable orbit?

Problem 2:

Stars often occur in pairs revolving around their common center of mass.  If one of the stars is a black hole, it is invisible.  Explain how the existence of such a black hole might be inferred from the light observed from the other, visible star.

Problem 3:

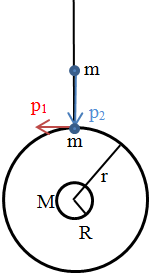A satellite is in a circular orbit of radius r around an airless spherical planet of radius R.  An asteroid of equal mass falls radially towards the planet, starting at zero velocity from a very large distance.  The satellite and the asteroid collide inelastically and stick together, moving in a new orbit that just misses the planet's surface.  What was the radius r of the satellite's original circular orbit in terms of R?

Problem 4:

Two particles with the same mass m orbit a massive planet of mass M >> m and radius R.  The orbit of one of the particles is circular, with radius 4R.  The other particle's orbits in the same plane, but its orbit is elliptical with semi-major axis 8R and r_min = 4R.  The angular momenta of the two particles point in opposite directions.  The particles collide and stick together, forming a new object.
(a)  What is the semi-major axis of the orbit of the new object in terms of R?
(b)  Does the new object collide with the planet?