Problem 1:

A particle of mass m moves in a central potential U(r) = kr²e^-r/a, with k and a positive constants.
(a)  Write down the Lagrangian for this system and determine the second-order equations of motion in polar coordinates. 
(b)  For what values of b is a circular orbit of radius b possible?
(c)  For a circular orbit of radius a, write down the angular momentum M in terms of m, k and a.
(d)  Is a circular orbit of radius a a stable orbit?

Solution:

• Concept:
  Motion in a central potential,  Lagrange's equations, stable orbits
• Reasoning:
  We are asked to write down the Lagrangian, and investigate the stability of a circular.
• Details of the calculation:
  (a)  L = T - U = ½m[(dr/dt)² + r²(dΦ/dt)²] - kr²e^-r/a.
  The generalized coordinates are r and Φ.  The coordinate Φ is cyclic.
  Lagrange's equations yield the equations of motion.
  (d/dt)[mr²(dΦ/dt)] = 0.  mr²(dΦ/dt) = M = constant.
  md²r/dt² - M/(mr³) = f(r),  md²r/dt² = M²/mr³ - 2kre^-r/a + (kr²/a)e^-r/a,
  or md²r/dt² = -dU_eff/dr.
  (b)  For a circular orbit of radius b we need md²r/dt²|_b = 0.
  We need 2kbe^-b/a - (kb²/a)e^-b/a > 0, or 2 - (b/a) > 0, or b < 2a.
  
  (c)  For a circular orbit of radius a we have M² = kma⁴e^-1.
  
  (d)  For a stable orbit we need a restoring force.  Let r = a + ρ, r >> ρ.
  We need md²ρ/dt² = -αρ.
  md²ρ/dt² = -∂U_eff(ρ)/∂ρ = -(∂U_eff/∂ρ)|_ρ=0 - (∂²U_eff/∂ρ²)|_ρ=0ρ (series expansion).
  We need ∂²U_eff/∂ρ² > 0 at ρ = 0, or ∂²U_eff/∂r² > 0 at r = a.
  ∂U_eff(r)/∂r =  -M²/mr³ + 2kre^-r/a - (kr²/a)e^-r/a.
  
  ∂²Ueff/∂r² = 3M²/mr⁴ + 2ke^-r/a - 2k(r/a)e^-r/a - (2kr/a)e^-r/a +  (kr²/a²)e^-r/a.
  ∂²Ueff/∂r²|_r=a = 3M²/ma⁴ - ke^-1 > 0.
  Inserting M² from above we have 3ke^-1 - ke^-1 > 0.
  The orbit is stable.

Problem 2:

Stars often occur in pairs revolving around their common center of mass.  If one of the stars is a black hole, it is invisible.  Explain how the existence of such a black hole might be inferred from the light observed from the other, visible star.

Solution:

• Concepts:
  The Doppler shift
• Reasoning:
  If the normal to the orbital plane is oriented roughly perpendicular to the line of sight, then the companion star recedes and approaches the observer in a periodic fashion.  The period and speed of the companion star can be measure, and the mass of the system m₁ + m₂ and the separation r of the star and the black hole can be calculated.
• Details of the calculation:
  A full understanding requires general relativity, but assume Newtonian mechanics and Newtonian gravity as a first approximation for the orbital motion.
  U(r) =  Gm₁m₂/r,  r = distance between the centers.
  μv²/r  = Gm₁m₂/r².  μ = m₁m₂/(m₁ + m₂),  v² = G(m₁ + m₂)/r.
  2πr/T = v.  Solve the two equations for the two unknowns, (m₁ + m₂) and r.
  r = vT/(2π), m₁ + m₂ = v³T/(2π G).
  Using the mass-luminosity relationship to estimate the mass of the visible star, the mass of the black hole can also be estimated.

Problem 3:

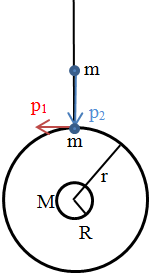A satellite is in a circular orbit of radius r around an airless spherical planet of radius R.  An asteroid of equal mass falls radially towards the planet, starting at zero velocity from a very large distance.  The satellite and the asteroid collide inelastically and stick together, moving in a new orbit that just misses the planet's surface.  What was the radius r of the satellite's original circular orbit in terms of R?

Solution:

• Concepts:
  Kepler orbits
• Reasoning:
  Since M >> m, assume the CM is the center of the planet.  For a single object moving in a central potential the energy E and the angular momentum L are conserved.  The motion is in a plane. For an object with mass m' in a circular orbit about a fixed center with mass M we have
  T = ½m'v² = ½GMm'/r,  U = -GMm'/r,  E = -½GMm'/r, 
  p = m'v = (GMm'²/r)^½,  L = rp = (GMm'²r)^½.
  In an inelastic collision momentum and angular momentum are conserved.
• Details of the calculation:
  Just before the collision:
  For the orbiting mass m, E₁ = -½GMm/r,  T₁ = ½GMm/r,  p₁ = (GMm²/r)^½,  L₁ = (GMm²r)^½.
  For the falling mass m, E₂ = 0,  T₂ = GMm/r,  p₂ = (2GMm²/r)^½,  L₂ = 0.

  Just after the collision:
  Momentum and angular momentum are conserved in the totally inelastic collision.  The momenta of the two colliding objects are perpendicular to each other.  Therefore the magnitude of the momentum of the combined mass is p = (p₁² + p₂²)^½,  p² = 3GMm²/r.
  The magnitude of the angular momentum of the combined object is  L = (GMm²r)^½.
  Its energy is E = T + U = p²/4m - 2GMm/r = -(5/4)GMm/r.
  
  From now on we have motion of a single object in a central potential.
  Energy and angular momentum are conserved.
  At the distance of closest approach L = p_maxr_min = p_maxR = (GMm²r)^½, p_max²R² = GMm²r.
  E = p_max²/(4m) - 2GMm/R = -(5/4)GMm/r.
  GMm²r/(4mR²) - 2GMm/R = -(5/4)GMm/r.
  r² - 8Rr + 5R² = 0,  r = 4R ± √(11)R.
  The perihelion of the orbit is at R, so r > R.
  r =  4R + √(11)R.