Problem 1:

A static charge distribution produces a radial electric field
E = (A/r²)exp(-br) e_r.
where A and b are constants.
(a)  What is the charge density?  Sketch it.
(b)  What is the total charge Q?

Problem 2:

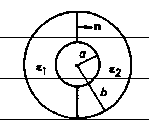One half of the region between the plates of a spherical capacitor of inner and outer radii a and b is filled with a linear isotropic dielectric of permittivity ε₁ and the other half has permittivity ε₂, as shown in figure.  If the inner plate has total charge Q and the outer plate has total charge -Q, find
(a)  the electric displacements D₁ and D₂ in the region of ε₁ and ε₂,
(b)  the electric fields in the region of ε₁ and ε₂,
(c)  and the total capacitance of this system.

Problem 3:

A parallel plate capacitor has square plates of width w and plate separation d.  A square dielectric also of width w and thickness d, with permittivity ε and mass m, is inserted between the plates a distance x into the capacitor and held there.  The plates are connected to a battery with battery voltage V₀.

(a)  Derive a formula for the force exerted on the dielectric as a function of x   Neglect edge effects. 
Assume that the battery stays connected and the dielectric is released from rest at x = w/2.  Describe its subsequent motion.
What is the range of the dielectric's motion, and within that range, what is the dielectric's speed as a function of position x? 
What is the maximum speed v_max of the dielectric?  Express your answers in terms of ε₀, ε, V₀, w, d and m.
(Neglect friction, ohmic heating, radiation.)

(b)  Now assume that the dielectric is released from rest at x = w/2 after the battery has been disconnected.
Derive a formula for the force exerted on the dielectric for w/2 < x < w.  Neglect edge effects. 
What is the maximum speed of the dielectric?  Express your answer in terms of ε₀, ε, V₀, w, d and m.

(c)  Find the ratio v_max(case a) to v_max(case b) in terms of ε₀ and ε.

Problem 4:

A long straight wire is connected to an ideal battery.  When the room temperature is 20.0 ^oC, the established temperature of the wire is 22.0 ^oC.
The wire is disconnected and one-third of it is cut off.  The remaining piece of the wire is then connected to the same battery in the same room.
What is the new established temperature of the wire?
Assume Newton's law of cooling applies, i.e. the rate at which a system transfers heat to its environment is proportional to the temperature difference between the system and its environment.