Consider a rectangular lamina with dimensions A and B, and mass M. The
lamina is attached to a wall with a nail placed at a point P = P(x,y), where the
coordinates x and y are referred to the center of the lamina.
(a) Determine the position of stable equilibrium.
(b) Describe the motion of the lamina when it is slightly displaced from this
equilibrium position.
A cylinder with mass m, radius R, and uniform density starts rolling without slipping from rest in a train that accelerates with constant acceleration a0. The axis of the cylinder is perpendicular to the motion of the train as shown below. Find the acceleration of the cylinder in the lab frame (rest frame) and in the train frame.

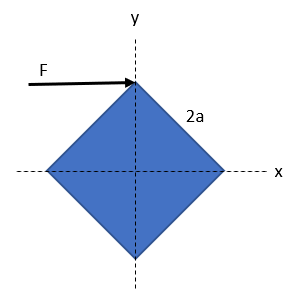
A square plate with uniform density, mass m, and of side length 2a, lies on a frictionless table as shown in the figure. A force F = F i is applied for a very short time Δt and delivers an impulse Δp to the upper corner. Find the position of this corner as a function of time.
You have a system of 4 particles of equal mass M = 1 kg. One sits at the origin
(x, y, z) = (0, 0, 0) m. The others sit at (1, 1, 0), (0, 1, 1) m, (1, 0, 1)
m. These particles are attached to each other by massless rigid rods such that
they will always maintain their positions relative to one another.
(a) Calculate the full moment of inertia tensor for this system.
(b) Find the principal axes for this system.
In case it's useful to you, here's a fact:
(4 − x)3 − 3(4 − x) − 2 = (2 − x)(5 − x)2.