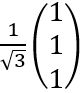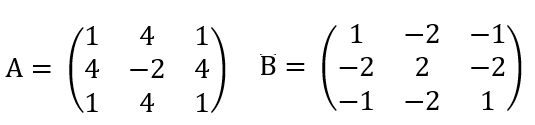
where a is a real number, in the orthonormal basis |1> and |2>.
A particle with mass m and with zero energy has a time-independent wave
function
ψ(x) = x exp(-x2/L2). Determine the potential
energy U(x) of the particle.
Solution:
A quantum mechanical system can be described by a Hamiltonian
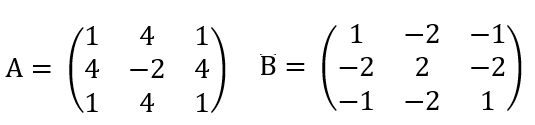
where a is a real number, in the orthonormal basis |1> and |2>.
(a) What are the energy
eigenvalues and normalized eigenvectors of this Hamiltonian?
(b) What is the probability for finding the system in state |2> at time t > 0
if the system is known to be in state |1> at t = 0?
Solution:
You prepare an ensemble of identical experiments at t = 0. You measure the values of a physical observable A at time t = t1 > 0 in all of the experiments of the ensemble. At time t2 > t1 you measure observable A again in all of the experiments - i.e., you follow the measurement at t = t1 in each experiment with a subsequent measurement of A in each experiment at t = t2.
True or False? Explain!
(a) The values you obtain for A across all of the experiments at time t = t1
are the same given you have made all of the measurements at the same time t = t1.
(b) The value you obtain for A in each experiment at t = t2 may be different
relative to the value obtained for A in the same experiment at t = t1.
(c) The expectation value of A is the same at both t = t1 and t = t2.
(d) The values you obtain for A in any of the experiments at either t = t1 or t = t2
must be one of the eigenvalues of its associated Hermitian operator.
At t = t3 > t2 you measure a second physical observable B across all of the
experiments - i.e., you follow the measurement of A at t = t2 in each experiment
with a measurement of B at t = t3 in each experiment. The commutator of the two
Hermitian operators associated with A and B satisfies the following: [A, B] ≠ 0.
True or False? Explain!
(e) The values you obtained for A at t = t2 in any of these experiments will
remain the same at t = t3 given you are measuring a different physical quantity B,
not A.
Solution:
In the Aharanov Bohm experiment, a beam of electrons is split in two and they pass on opposite sides of a very long solenoid of radius ra < r. The solenoid is centered at the origin of the x-y plane, is pointing along the z-axis, and is carrying a steady current I. The solenoid is infinitely long and the magnetic field inside is uniform. The magnetic field outside the solenoid is zero. The two beams (wave functions) acquire opposite phase shifts as they pass the solenoid along opposite sides on their way to the detector, resulting in an interference pattern. In this problem, we will calculate these phase shifts.
(a) Adopting the Coulomb gauge, show that the vector potential A for r > ra is given by
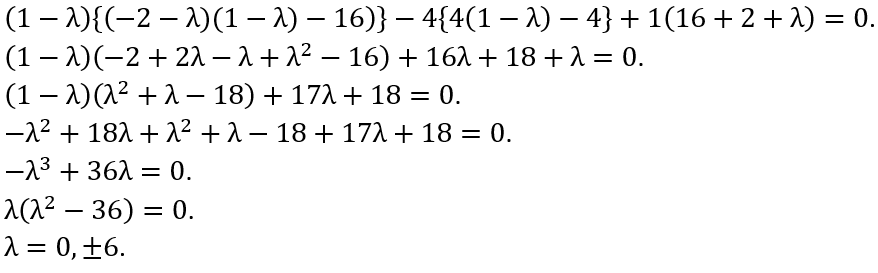
where φ is the azimuthal angle in the x-y plane and Φ is the magnetic flux through the solenoid.
(b) The classical Hamiltonian for a particle of charge q and momentum p in the presence of an electromagnetic field is given by
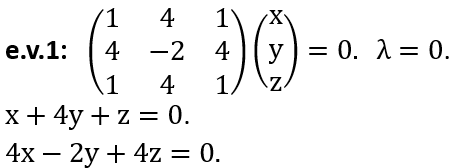
where A is the vector potential and V the scalar
potential.
Write down the time-dependent Schroedinger equation for a quantum particle of
charge q and wave function Ψ in the presence of an
electromagnetic field.
(c ) Let's define a new wave function
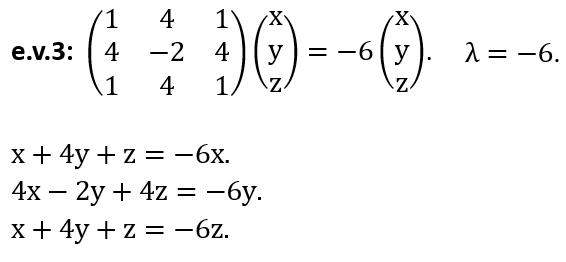
where r0 is some arbitrarily chosen reference
point. Using this definition, show that the Schroedinger equation for the new
wave function Ψ' reduces to a usual Schroedinger equation without the vector potential|A|.
(d) Back to the experiment. Before exiting the entrance slits, the beam is moving through a region with A = 0. Using the vector potential found in (a), show that the wave functions acquire a phase g = ±qΦ(2ħ), resulting in a (measurable) phase difference of (q/ħ)Φ as electrons pass the solenoid on opposite sides although the B field itself is zero.
(e) Based on these observations, does the vector potential have a physical meaning and is the quantum theory gauge invariant?
Solution: