More Problems

Problem 1:

The Sun is located 8 kiloparsecs (2.5*10²⁰ meters) from the center of the Milky Way.  Stars in the solar vicinity are, on average, moving in a circular orbit about the Galactic Center at a velocity of 225 kiloparsec/Gigayear (220 kilometers/second).  Calculate the mass of the galaxy interior to the solar orbit.

Solution:

• Concepts:
  The gravitational force, Gauss' law: 
• Reasoning:
  4πR²F/m = 4πGM_inside, for a spherically symmetric mass distribution.
• Details of the calculation:
  Let us assume a spherically symmetric mass distribution.
  v²/R = F/m = GM_inside/R²,   M_inside = Rv²/G. 
  Plug in numbers.
  M_inside = Rv²/G = (2.5*10²⁰ m)(2.2*10⁵ m/s)²/(6.674*10^-11m³/(kg s²)) = 1.81*10⁴¹ kg.

Problem 2:

A particle of mass m is given an initial velocity v₀i.  Assume that the particle is subject to a drag force F = -bv^½i.
(a)  Find v as a function of time.
(b)  How far does the particle travel before coming to rest?

Solution:

• Concepts:
  Newton's second law
• Reasoning:
  Given the acceleration and v(0) we can find v(t) and Δx(t) as a function of time.
• Details of the calculation:
  (a)  mdv/dt = -bv^½,  dv/dt = -(b/m)v^½,  dv/v^½  = -(b/m )t,
  ∫_v0^v(t) dv/v^½ = -(b/m) ∫₀^tdt = -bt/m,
  2(v(t)^½ - v₀^½) = -bt/m,
  v(t) = (v₀^½ - bt/(2m))².
  
  (b)  v(t) = 0 --> t_f = 2mv₀^½/b.
  After a time interval t_f the particle stops.  In the time interval t_f the particle travels a distance Δx.
  Δx = ∫₀^tfv(t) dt = ∫₀^tf(v₀^½ - bt/(2m))²dt = [(v₀^½ - bt_f/(2m))³- v₀^3/2]/(-3b/(2m)).
  Δx = 2mv₀^3/2/(3b).

Problem 3:

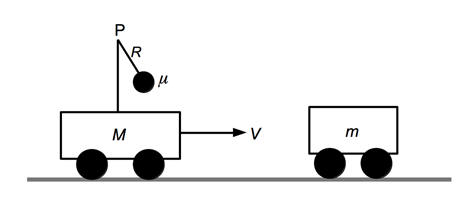
A cart of mass M has a pole mounted on it as illustrated in the figure.  Assume the pole mass is negligible.  A ball of mass μ hangs by a massless string, of length R, attached to the pole at point P.
(a)  Suppose the cart (of mass M) and the ball are initially at rest, with the ball hanging in its equilibrium position.  Calculate the minimum velocity that must be imparted to the ball for it to rotate in a circle of radius R in the vertical plane.
(b)  Now suppose the cart and ball have initial velocity V towards the right.  The cart crashes into a stationery cart of mass m and sticks to it.  Find the velocity of the system after a collision.  In this part and the next, neglect friction and assume that M, m >> μ.
(c)  Find the smallest value of the initial cart speed for which the ball can go in circles in the vertical plane following a collision.

Solution:

• Concepts:
  Inelastic collisions, Newton's laws, conservation of momentum, circular motion, frame transformations
• Reasoning:
  Before the collision cart 1 of mass M and mass μ move with uniform velocity v₁ = V.  The impulse of the collision changes the velocity of cart 1, and after the collision cart 1 moves with uniform velocity v₂.  The small mass moves with velocity v = v₁ - v₂ with respect to cart 1 immediately after the collision.  After the collision the rest frame of cart 1 is an inertial frame and we can analyze the problem in that frame.
  Note:  We make use that μ is negligible compared to M and m.  After the collision the center of mass of the system moves with constant velocity.  The position of the CM changes if μ oscillates.  We neglect this.
• Details of the calculation:
  (a)  The forces on the ball are the force of gravity and the tension from the string.  If the initial speed is large enough so that the ball gains a height greater than R, then the centripetal acceleration needed to keep the ball moving on the circle is partly provided by gravity and the tension decreases.  When the tension vanishes then the ball behaves like a free particle in a gravitational field.
  The ball can rotate in a circle if the centripetal acceleration v_top²/R > g.
  Then ½μv² = 2μgR + ½μv_top² > 2μgR + ½μgR = (5/2)μgR.  v_min = (5gR)^½.
  (b)  Conservation of momentum:  Mv₁ = (m + M)v₂,  v₂ = Mv₁/(m + M) = MV/(m + M).
  (c)  In the rest frame of cart 1 immediately after the collision we have a ball of mass μ on a string of length R moving with velocity v.
  v = v₁ - v₂ = mV/(M + m).
  When v > (5gR)^½, the ball can go in circles in the vertical plane following a collision.
  Therefore for V > (M + m)v/m  = (M + m)(5gR)^½/m the ball can go in circles in the vertical plane following a collision.