More Problems

Review Problems

Problem 1:

A particle of mass M and relativistic momentum p decays in flight into two particles of mass m. Both particles of mass m move with momentum p' making an angle θ with respect to the direction of p. Find M in terms of m, p', and θ.

Solution:

Concepts:
Relativistic collisions, energy and momentum conservation
Reasoning:
The decay of a particle is a relativistic problem. In relativistic "collisions" energy and momentum are always conserved.
Details of the calculation:
Energy conservation: M²c⁴ + p²c² = 4(m²c⁴ + p'²c²).
Momentum conservation: p = 2p'cosθ.
Algebra: M²c⁴ + 4p'²c²cos²θ = 4m²c⁴ + 4p'²c².
M²c⁴ = 4m²c⁴ + 4p'²c² - 4p'²c²cos²θ = 4m²c⁴ + 4p'²c²(1 - cos²θ).
M² = 4m² + (4p'/c²)(1 - cos²θ). M = 2(m² + (p'/c²)sin²θ)^½.

Problem 2:

In his acceptance speech for the Royal Society's Copley Medal on November 30, 2006 Professor Stephen Hawking said that humans must colonize other planets in other solar system, or otherwise face extinction by one disaster or another. However, using conventional, chemical-fuel rockets and leaving the solar system with a speed of about 25 km/s, it would take 50000 years to get to the nearest star. But by using matter/antimatter annihilation, speeds close to the speed of light could be reached, making it possible to get to the nearest star in about 6 years.
(a) How fast would that spacecraft have to travel?
(b) How long would the one way trip appear to the passengers?

Solution:

Concepts:
The proper time interval
Reasoning:
We are asked calculate the proper time interval in the spacecraft frame, given the time interval in the earth fame.
Details of the calculation:
(a) Assumed distance to nearest star:
vt = (25000 m/s)*(50000 y)*(365 day/y)*(24 h/day)*(3600 s/h)
= 3.94*10¹⁶ m = 4.16 ly.
To travel this distance in 6 years the speed of the spacecraft would have to be
v = (25000 m/s)*(50000 y)/(6 y) = 0.694 c.
(b) Proper time τ = t/γ = (6y)*(1 - 0.694²)^½ = 4.32 y.

Problem 3:

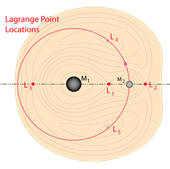
The Lagrange points are points of equilibrium for small-mass objects under the gravitational influence of two massive orbiting bodies. There are five special points where an object placed at any one of these points will be at rest in the rotating reference frame.

Assume M₂ orbits M₁ in a circular orbit of radius R, in the rest frame of M₁. Let M₁ = M and M₂ = M/10. Find the approximate location of the Lagrange point L₁ and L₂ using M₂ << M₁. (Make reasonable approximations.)

Solution:

Concepts:
Two interacting masses, motion in a central potential, non-inertial frames
Reasoning:
M₁ and M₂ orbit their CM. The problem of two interacting particles in their CM frame is equivalent to the problem of a fictitious particle of reduced mass μ moving in a central potential with potential energy U(r).
Here μ = M₁M₂/(M₁ + M₂) = M/11.
Details of the calculation:
U = GM²/(10R). F = GM²/(10R²) = (M/11)v²/R = (M/11)ω²R. ω² = 11GM/(10R³).
The CM frame is rotating with angular frequency ω.

For a small mass m to be at rest at L₁ in the rotating CM frame a distance r from M₂ we need the vector sum of the gravitational forces and the fictitious centrifugal force to be zero.
-GMm/(R - r)² + mω²(R - r) + GMm/(10r²) = 0.
1/(R - r)² - 11(R - r)/(10R³) - 1/(10r²) = 0.

Now we have to make reasonable approximations.
Using M₁ >> M₂ we set 11/10 ≈ 1. We also assume R >> r. Then
(1 + 2r/R)/R² - 1/(10r²) ≈ (R - r)/R³.
(1 + 2r/R)/R² - 1/(10r²) ≈ 1/R².
2r/R³ ≈ 1/(10r²).
r ≈ R/2.714 ≈ 0.368 R

For a small mass m to be at rest at L₂ in the rotating CM frame a distance r from M₂ we need
-GMm/(R + r)² + mω²(R + r) - GMm/(10r²) = 0.
1/(R + r)² - (11/10)(R + r)/r³ + 1/(10r²) = 0.
(1 - 2r/R)/R² + 1/(10r²) ≈ 1/R².

Problem 4:

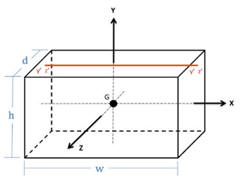
Assume a rectangular box of mass M and uniform density is suspended from a rod intersecting two of its faces as shown in the figure in a uniform gravitational field. The intersection points have coordinates (±w/2, y', z'). The gravitational acceleration is -g j. The box can rotate without friction about the rod. What is the frequency of small oscillation of the box about its equilibrium position?

Solution:

Concepts:
Small displacements from stable equilibrium
Reasoning:
The potential energy has a minimum at the position of stable equilibrium.
Details of the calculation:
(a) Potential energy: U = -Mgd'cosθ = -Mg(y'² + z'²)^½cosθ.

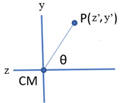
Extreme U: dU/dθ = 0, sinθ = 0, θ = 0 or π.

θ = π, CM lies directly above the pivot point --> unstable equilibrium.
θ = 0, CM lies directly below the pivot point --> stable equilibrium.

For small angles θ near θ = 0 we have U(θ) = U(0) + dU/dθ|₀θ + ½ d²U/dθ²|₀θ² + ... .
d²U/dθ² = Mgd'cosθ. U(θ) = U(0) + ½Mgd'θ², keeping only terms up to second order in θ.
U(θ) = U(0) + ½kθ² with k = Mgd'.
τ = I d²θ/dt² = -dU/dθ = -Mgd'θ. We have a restoring torque.
To find I we use the parallel axis theorem.
I_xx(CM) = (M/12)(h² + d²). I(y',z') = I_xxCM + M(y'² + z'²) = M(h²/12 + d²/12 + y'² + z'²).
d²θ/dt² = -g(y'² + z²)^½(h²/12 + d²/12 + x² + y²)θ.
Frequency of oscillations: ω² = g(y'² + z'²)^½(h²/12 + h²/12 + y'² + z'²).

Problem 5:

A particle of mass m moves in one dimension. It is remarked that the exact eigenfunction for the ground state is Ψ(x) = A/cosh(λx), where λ is a constant and A is the normalization constant. Assuming that the potential U(x) energy vanishes at infinity, derive the ground state energy and also U(x).

Solution:

Concepts:
The time-independent Schroedinger equation
Reasoning:
If ψ(x) and E are given, we can solve for U(x).
Details of the calculation:
The given wave function is a solution of the 1-dimensional, time-independent Schroedinger equation.
(-ħ²/2m)(∂²/∂x²)Ψ(x) + U(x)Ψ(x) = EΨ(x).
(∂/∂x)(1/cosh(λx)) = -(sinh(λx)/cosh²(λx))λ.
(∂²/∂x²)(1/cosh(λx)) = -(λ²/cosh(λx))[1 - 2sinh²(λx)/cosh²(λx)].
(ħ²/2m)Aλ²/cosh(λx))[1 - 2sinh²(λx)/cosh²(λx)] + U(x)A/cosh(λx) = EA/cosh(λx).
(ħ²λ²/2m)[1 - 2sinh²(λx)/cosh²(λx)] = E - U(x).
As x --> ∞, U(x) --> 0, and sinh(λx)/cosh(λx) --> 1. Therefore E = -(ħ²λ²/2m).
U(x) = -(ħ²λ²/m) + (ħ²λ²/m) sinh²(λx)/cosh²(λx)] = -(ħ²λ²/m)(1/cosh²(λx)]).