More Problems

Problem 1:

A long coaxial cable carries a uniform volume charge density ρ on the inner cylinder (radius a), and a uniform surface charge density on the outer cylindrical shell (radius b).  This surface charge is negative and is of just the right magnitude that the cable as a whole is electrically neutral.

         

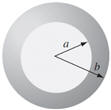
(a)  Find the electric field inside the inner cylinder (r < a).
(b)  Find the electric field between the cylinders (a < r < b).
(c)  Find the electric field outside the cable (r > b).

Solution:

• Concepts:
  Gauss' law
• Reasoning:
  The problem has enough symmetry to find E(r) from Gauss' law alone.
  Choose cylindrical coordinates.  Then E will only have a radial component,
  E = E(r) (r/r).
• Details of the calculation:
  r < a:  E*2πr* l = Q_insidel/ε₀ = ρπr²l/ε₀.  E(r) = ρr/(2ε₀) e_r.
  a < r < b:  E*2πr = ρπa²l/ε₀.  E(r) = ρa²/(2ε₀r) e_r.
  r > b:  E(r) = 0.
  
  

Problem 2:

Two large parallel metal plates of area A are separated by a distance d, small compared to the size of the plates.  The distance d is small enough that the plates can be treated as if they were infinite in extent.  A battery maintains a potential difference V across the plates.  An external agent slowly inserts an uncharged conducting slab of the same area A and  thickness d/2 is midway between the two plates, not touching either of them.  After the slab has been inserted, it is held in place at rest.
(a)  What is the capacitance of the configuration before and after the slab is inserted?
(b)  How much work was done by the external agent inserting the slab?

Solution:

• Concepts:
  Capacitance, energy and work
• Reasoning:
  We must find the ΔW_mech, the work done by the external agents as the slab is inserted into a capacitor and the capacitance changes.
• Details of the calculation:
  (a)  After the slab has been inserted, we have two parallel plate capacitors in series.
  For these capacitor we have
  C₁ = C₂ = ε₀A/(d/4).
  C_before = ε₀A/d.   1/C_after = 1/C₁ + 1/C₂.  C_after = 2ε₀A/d.
  (b)  Total energy store in the capacitor:  U = ½CV₀².
  Let ΔC = C_after - C_before = ε₀A/d.
  ΔW_mech + ΔW_bat = ΔU.  ΔW_bat = ΔQV = ΔCV².  ΔU = ½ΔCV². 
  ΔW_mech = -½ΔCV² = -½ε₀AV²/d.
  The external agent did negative work.

Problem 3:

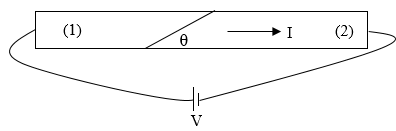
A very long, straight wire with circular cross section A is made from two different materials with permittivities ε₁ and ε₂ and conductivities σ₁ and σ₂, respectively, spliced together at an angle θ.  The wire is connected to a battery, and a current I flows in the wire.  Assume the microscopic form of Ohm's law holds in each material.  Assume the current density is uniform over a cross-sectional area of the wire.  (Since the wire is very long, the geometry of the ends can be ignored.)
(a)  What is the free charge density at the splice?
(b)  What is the bound charge density at the splice?
(c)  What is the bound charge density at the splice on the material 2 side?

Solution:

• Concepts:
  Ohm's law, Gauss' law
• Reasoning:
  j = σE,  (D₂ - D₁)∙n₂ = β_free,   (E₂ - E₁)∙n₂ = β_total/ε₀.
  (Denote the surface charge density by β, since the symbol σ is already in use.)
• Details of the calculation:
  (a)  j = I/A.  ∇∙j = 0, there are no sources or sinks.  j₁∙n₂ = j₂∙n₂ = j sinθ.
  (D₂ - D₁)∙n₂ = β_free,  (ε₂E₂ - ε₁E₁)∙n₂ = β_free,  ((ε₂/σ₂)j - (ε₁/σ₁)j)∙n₂ =  β_free.
  β_free = (ε₂/σ₂ - ε₁/σ₁) (I sinθ)/A.
  
  (b)  β_total = (ε₀/σ₂ - ε₀/σ₁) (I sinθ)/A.
  β_bound =  β_total -  β_free =  -((ε₂ - ε₀)/σ₂ - (ε₁ - ε₀)/σ₁) (I sinθ)/A.
  
  (c) P₂ =  ε₀χ₂E₂ =  (ε₂ - ε₀)E₂.  P₂∙n₂ = β_bound(2).
  β_bound(2) = -(ε₂ - ε₀)(I sinθ)/(Aσ₂).
  β_bound(1) = (ε₁ - ε₀)(I sinθ)/(Aσ₁).